Задача №200. Расчёт максимальной суммы налогового сбора

Рынок товара А представлен следующими функциями спроса и предложения:

Q_D = 400 – 10Р;

Q_S = – 500 + 20Р.

Определите, какую максимальную сумму налога можно собрать с этого рынка путем взимания акциза с каждой проданной  единицы товара А?

Решение:

Найдём первоначальное равновесие на рынке. Приравняем функции спроса и предложения:

Q_D = Q_S

400 – 10Р = – 500 + 20Р

30Р = 900

Р_E = 30 - равновесная цена,

Q_E = 400 – 10 × 30 = 100 - равновесный объём.

Изобразим ситуацию графически. Найдём координаты точек пересечения графиков функций с осью ординат.

При Q = 0 функция спроса пересекает ось ординат в точке А.

400 – 10Р = 0

Р = 40

При Q = 0 функция предложения пересекает ось ординат в точке С:

– 500 + 20Р = 0

Р = 25

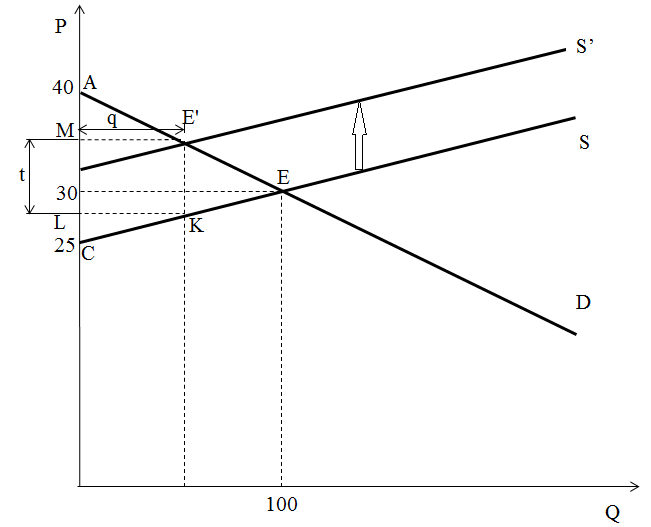
Если государство будет взимать акциз с каждой проданной единицы товара А, то кривая предложения сдвинется вверх на величину акциза в положение S’.

Графически сумма налоговых сборов  будет представлена площадью прямоугольника ME’KL, вписанного в треугольник АЕС.

Чтобы найти максимальную сумму налога, необходимо найти функцию площади прямоугольника и решить задачу на максимум функции.

Высота треугольника АЕС равна 100, а основание (40 – 25) = 15

Пусть t, q – длины сторон прямоугольника.

Боковая сторона прямоугольника КЕ’ отсекает ΔКЕ’E, подобный данному ΔAEC.

Высоты в этих треугольниках пропорциональны основаниям, поэтому можно записать:

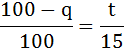
Отсюда находим t:

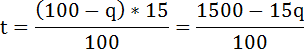
Площадь искомого прямоугольника ME’KL:

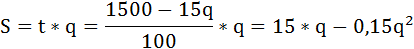
Найдём максимум этой функции. Для этого определим её производную и приравняем её к нулю.

S’ = 0

15 – 2 × 0,15q = 0

15 = 2 × 0,15q

q = 50

Тогда наибольшее значение  функции S при q = 50, равно:

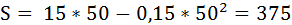
Акциз при этом будет равен:

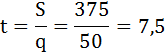
Итак, максимальная сумма налоговых сборов равна 375, при акцизе 7,5 с каждой проданной единицы товара.