Задача №60. Расчёт изменения скорости оборота денег
В обороте находится 3,5 млн. товаров по цене 420 рублей за единицу. В среднем каждый рубль 3 раза использовался для приобретения товаров. При условии, что цена товара выросла на 200 рублей, а количество товаров и денег в обращении осталось неизменным, определите, как должна измениться скорость оборота денежных знаков.
Решение:
Решим эту задачу двумя способами.
Способ I
Воспользуемся уравнением обмена:
MV = PQ,
где
М (money) – масса денег в обороте;
V (velosity) – скорость оборота денег;
P (price) – средняя цена товаров и услуг;
Q (quantity) – количество реализованных товаров и услуг (физический объём производства).
Отсюда
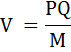
Зависимость между динамикой уровня цен, объёма денежной массы, скорости оборота денег и объёма производства можно записать в виде выражения:
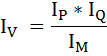
где
IV – индекс оборачиваемости (количества оборотов) денежной массы;
IP – индекс цен,
IM – индекс объёма денежной массы,
IQ – индекс физического объёма.
Индекс – это относительная величина, которая характеризует изменение исследуемого явления во времени, в пространстве или по сравнению с некоторым эталоном.
Цена товара была 420 рублей, выросла на 200 рублей, следовательно, стала равна 620 рублей. Находим отношение цены в текущем периоде к цене базисного периода, получаем индивидуальный индекс цен.
Количество товаров и денег в обращении осталось неизменным, следовательно, соответствующие индексы равны 1.
Рассчитаем индекс оборачиваемости (количества оборотов) денежной массы:
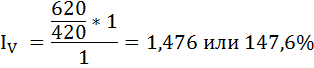
Следовательно, скорость оборота денег увеличилась на 47,6%.
Способ II
Воспользуемся тем же уравнением обмена:
MV = PQ,
подставим имеющиеся данные до повышения цены
3*M= 3,5 * 420
3*M= 1470
M = 490.
Так как количество товаров и денег в обращении осталось неизменным, следовательно,
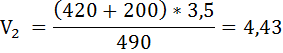
Так как V1 = 3, следовательно, прирост скорости оборота составит 47,6%:
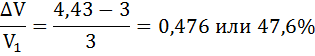

Рыночное равновесие
Смотри ещё
- Анализ хозяйственной деятельности / Задача №5. Расчёт изменения общей себестоимости продукции за счет влияния факторов и их долевое участие в общем изменении
- Деньги, банковская система и монетарная политика / Задача №10. Расчёт изменения предложения денег и величины банковского мультипликатора
- Деньги, банковская система и монетарная политика / Задача №13. Расчёт фактических резервов банка, расчёт объёма кредитов банка, расчёт изменения денежной массы
- Деньги, банковская система и монетарная политика / Задача №34. Расчёт темпа инфляции в количественной теории денег
- Деньги, банковская система и монетарная политика / Задача №66. Расчёт суммы долга по товарам, проданным в кредит
- Деньги, банковская система и монетарная политика / Задача №69. Расчёт избыточной денежной массы
- Деньги, банковская система и монетарная политика / Задача №82. Расчёт объёма депозитов
- Индексы / Задача №40. Расчёт индивидуальных индексов цен, физического объёма, товарооборота
- Индексы / Задача №41. Расчёт изменения товарооборота в относительном и абсолютном выражении
- Индексы / Задача №42. Расчёт индекса цен по формуле Пааше
- Индексы / Задача №44. Расчёт индекса цен
- Статистика оплаты труда и затрат на рабочую силу / Задача №26. Расчёт фонда заработной платы
- Статистика производительности труда / Задача №27. Расчёт изменения затрат труда
- Статистика уровня жизни населения / Задача №31. Расчёт индекса покупательной способности рубля






















