Задача №43. Расчёт описательных статистик

Компания Zagat публикует рейтинги ресторанов, расположенных в разных городах США.

В таблице содержатся оценки качества пищи, оформления блюд, уровня обслуживания и стоимость обеда для одного человека в 200 ресторанах Нью-Йорк Сити (NYC) и Лонг-Айленда (LI).

	Город	Пища	Оформление	Обслуживание	Суммарный рейтинг	Цена
1	NYC	19	21	18	58	50
2	NYC	18	17	17	52	38
3	NYC	19	16	19	54	43
4	NYC	23	18	21	62	56
5	NYC	23	20	21	64	51
6	NYC	23	18	20	61	36
7	NYC	20	17	16	53	25
8	NYC	20	15	17	52	33
9	NYC	19	18	18	55	41
10	NYC	21	19	19	59	44
11	NYC	20	17	16	53	34
12	NYC	21	23	21	65	39
13	NYC	24	20	22	66	49
14	NYC	20	17	20	57	37
15	NYC	17	18	14	49	40
16	NYC	21	17	20	58	50
17	NYC	21	19	21	61	50
18	NYC	20	16	19	55	35
19	NYC	17	11	13	41	22
20	NYC	21	16	20	57	45
21	NYC	23	20	23	66	44
22	NYC	17	19	16	52	38
23	NYC	22	14	15	51	14
24	NYC	19	19	18	56	44
25	NYC	21	19	20	60	51
26	NYC	19	14	16	49	27
27	NYC	19	17	19	55	44
28	NYC	21	13	21	55	39
29	NYC	24	21	21	66	50
30	NYC	19	16	19	54	35
31	NYC	17	15	15	47	31
32	NYC	19	16	19	54	34
33	NYC	22	19	21	62	48
34	NYC	22	18	20	60	48
35	NYC	14	15	15	44	30
36	NYC	22	22	21	65	42
37	NYC	20	15	18	53	26
38	NYC	18	14	17	49	35
39	NYC	18	20	16	54	32
40	NYC	24	18	21	63	63
41	NYC	21	17	18	56	36
42	NYC	18	17	17	52	38
43	NYC	20	19	19	58	53
44	NYC	21	10	17	48	23
45	NYC	19	14	19	52	39
46	NYC	18	17	17	52	45
47	NYC	20	16	17	53	37
48	NYC	21	12	14	47	31
49	NYC	19	17	19	55	39
50	NYC	21	20	20	61	53
51	NYC	21	18	21	60	37
52	NYC	17	14	17	48	37
53	NYC	17	17	18	52	29
54	NYC	23	19	18	60	38
55	NYC	23	22	21	66	37
56	NYC	21	18	19	58	38
57	NYC	21	19	23	63	39
58	NYC	21	18	18	57	29
59	NYC	22	18	20	60	36
60	NYC	22	20	20	62	38
61	NYC	23	20	22	65	44
62	NYC	23	18	20	61	27
63	NYC	21	14	19	54	24
64	NYC	17	17	17	51	34
65	NYC	23	23	22	68	44
66	NYC	15	17	15	47	23
67	NYC	19	14	17	50	30
68	NYC	20	19	18	57	32
69	NYC	20	15	17	52	25
70	NYC	20	12	18	50	29
71	NYC	23	19	20	62	43
72	NYC	19	21	19	59	31
73	NYC	15	13	15	43	26
74	NYC	20	17	22	59	34
75	NYC	21	17	18	56	23
76	NYC	23	20	21	64	41
77	NYC	27	16	19	62	32
78	NYC	17	17	16	50	30
79	NYC	22	11	17	50	28
80	NYC	20	16	19	55	33
81	NYC	20	12	16	48	26
82	NYC	25	25	24	74	51
83	NYC	17	17	18	52	26
84	NYC	25	22	23	70	48
85	NYC	19	18	19	56	39
86	NYC	27	20	24	71	55
87	NYC	21	11	17	49	24
88	NYC	19	18	19	56	38
89	NYC	20	21	20	61	31
90	NYC	23	19	21	63	30
91	NYC	24	27	23	74	51
92	NYC	18	18	20	56	30
93	NYC	15	16	14	45	27
94	NYC	16	20	17	53	38
95	NYC	18	16	17	51	26
96	NYC	20	12	18	50	28
97	NYC	21	24	21	66	33
98	NYC	21	18	19	58	38
99	NYC	23	15	20	58	32
100	NYC	19	14	16	49	25
101	LI	22	24	21	61	53
102	LI	24	23	23	58	44
103	LI	23	20	23	58	47
104	LI	26	21	24	65	59
105	LI	30	27	28	71	58
106	LI	31	26	28	69	44
107	LI	30	27	26	63	35
108	LI	24	19	21	56	37
109	LI	24	23	23	60	46
110	LI	23	21	21	61	46
111	LI	25	22	21	58	39
112	LI	30	32	30	74	48
113	LI	29	25	27	71	54
114	LI	23	20	23	60	40
115	LI	23	24	20	55	46
116	LI	22	18	21	59	51
117	LI	26	24	26	66	55
118	LI	29	25	28	64	44
119	LI	26	20	22	50	31
120	LI	30	25	29	66	54
121	LI	31	28	31	74	52
122	LI	21	23	20	56	42
123	LI	30	22	23	59	22
124	LI	26	26	25	63	51
125	LI	24	22	23	63	54
126	LI	25	20	22	55	33
127	LI	28	26	28	64	53
128	LI	29	21	29	63	47
129	LI	31	28	28	73	57
130	LI	20	17	20	55	36
131	LI	20	18	18	50	34
132	LI	25	22	25	60	40
133	LI	25	22	24	65	51
134	LI	30	26	28	68	56
135	LI	22	23	23	52	38
136	LI	29	29	28	72	49
137	LI	28	23	26	61	34
138	LI	22	18	21	53	39
139	LI	28	30	26	64	42
140	LI	27	21	24	66	66
141	LI	29	25	26	64	44
142	LI	19	18	18	53	39
143	LI	30	29	29	68	63
144	LI	26	15	22	53	28
145	LI	22	17	22	55	42
146	LI	22	21	21	56	49
147	LI	29	25	26	62	46
148	LI	26	17	19	52	36
149	LI	28	26	28	64	48
150	LI	26	25	25	66	58
151	LI	28	25	28	67	44
152	LI	25	22	25	56	45
153	LI	26	26	27	61	38
154	LI	25	21	20	62	40
155	LI	28	27	26	71	42
156	LI	30	27	28	67	47
157	LI	26	24	28	68	44
158	LI	30	27	27	66	38
159	LI	26	22	24	64	40
160	LI	30	28	28	70	46
161	LI	31	28	30	73	52
162	LI	31	26	28	69	35
163	LI	25	18	23	58	28
164	LI	20	20	20	54	37
165	LI	25	25	24	70	46
166	LI	22	24	22	54	30
167	LI	23	18	21	54	34
168	LI	22	21	20	59	34
169	LI	30	25	27	62	35
170	LI	22	14	20	52	31
171	LI	32	28	29	71	52
172	LI	20	22	20	60	32
173	LI	19	17	19	47	30
174	LI	29	26	31	68	43
175	LI	30	26	27	65	32
176	LI	24	21	22	65	42
177	LI	34	23	26	69	39
178	LI	24	24	23	57	37
179	LI	32	21	27	60	38
180	LI	22	18	21	57	35
181	LI	23	15	19	51	29
182	LI	29	29	28	78	55
183	LI	25	25	26	60	34
184	LI	28	25	26	73	51
185	LI	27	26	27	64	47
186	LI	29	22	26	73	57
187	LI	22	12	18	50	25
188	LI	22	21	22	59	41
189	LI	24	25	24	65	35
190	LI	27	23	25	67	34
191	LI	25	28	24	75	52
192	LI	19	19	21	57	31
193	LI	18	19	17	48	30
194	LI	18	22	19	55	40
195	LI	26	24	25	59	34
196	LI	20	12	18	50	28
197	LI	25	28	25	70	37
198	LI	29	26	27	66	46
199	LI	23	15	20	58	32
200	LI	28	23	25	58	34

1. Вычислите среднее арифметическое и медиану каждого показателя для двух групп ресторанов.

2. Вычислите первый и третий квартили каждого показателя для двух групп ресторанов.

3. Определите размах, дисперсию, стандартное отклонение и коэффициент вариации каждого показателя для двух групп ресторанов.

4. Являются ли эти данные асимметричными? Если да, определите вид асимметрии.

5. Постройте блочные диаграммы выборок каждого показателя для двух групп ресторанов.

6. Определите коэффициенты корреляции. Постройте матрицы коэффициентов парной корреляции для показателей двух групп ресторанов. Сделайте выводы.

Решение:

1. Рассчитаем среднее арифметическое значение оценок каждого показателя для групп ресторанов по формуле:

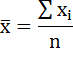
Формула средней арифметической простой

Среднее арифметическое значение бальных оценок качества пищи для ресторанов Нью-Йорк Сити равно:

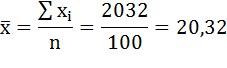
Расчёт средней арифметической простой

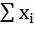Сумма значений признака – суммарное значение бальных оценок,

n – количество ресторанов.

Аналогично произведём расчёт средних по другим критериям оценок по обеим группам. Результаты вычислений занесём в таблицы 1 и 2.

Таблица 1 Описательные статистики для группы ресторанов Нью-Йорк Сити
Описательная статистика	Значение показателя
Описательная статистика	Пища	Оформление	Обслуживание	Суммарный рейтинг	Цена
Сумма	2032	1738	1872	5642	3674
Число наблюдений	100	100	100	100	100
Среднее арифметическое	20,32	17,38	18,72	56,42	36,74
Медиана	20	17	19	56	37
Мода	21	17	19	52	38
Квартиль первый	19	16	17	52	33
Квартиль третий	22	19	20	61	43,5
Межквартильный размах	3	3	3	9	10,5
Минимум	14	10	13	41	14
Максимум	27	27	24	74	63
Размах вариации	13	17	11	33	49
Дисперсия выборки	6,24	9,672323	5,53697	45,07434	84,69939
Стандартное отклонение	2,4979992	3,110036	2,353077	6,713743	9,203227
Коэффициент вариации	12,29	17,89	12,57	11,9	25,05

Таблица 2 Описательные статистики для группы ресторанов Лонг-Айленда
Описательная статистика	Значение показателя
Описательная статистика	Пища	Оформление	Обслуживание	Суммарный рейтинг	Цена
Сумма	2576	2282	2416	6186	4218
Число наблюдений	100	100	100	100	100
Среднее арифметическое	25,76	22,82	24,16	61,86	42,18
Медиана	26	23	24	62	42
Мода	22	25	28	64	34
Квартиль первый	23	20,5	21	56,5	35
Квартиль третий	29	26	27	67	48,5
Межквартильный размах	6	5,5	6	10,5	13,5
Минимум	18	12	17	47	22
Максимум	34	32	31	78	66
Размах вариации	16	20	14	31	44
Дисперсия выборки	13,59838	16,37131	11,91354	48,84889	83,68444
Стандартное отклонение	3,687599	4,046148	3,451599	6,989198	9,14792
Коэффициент вариации	14,32	17,73	14,29	11,3	21,69

По результатам расчётов делаем вывод, что посетители ресторанов Лонг-Айленда дали в среднем более высокую оценку качеству пищи, оформлению и обслуживанию, чем посетители ресторанов Нью-Йорк Сити.

Для более точных выводов о средних значениях найдём медиану.

Медианой называется число, разделяющее дискретный ряд пополам.

Для нахождения медианы варианты дискретного ряда ранжируем, например, по возрастанию и выберем вариант, стоящий в середине полученного ряда.

Так как ряд распределения состоит из чётного числа вариантов (n=100), середина приходится на среднее значение 50-го и 51-го варианта.

Таким образом, медиана бальных оценок качества пищи 100 ресторанов Нью-Йорк Сити равна:

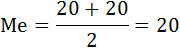
Расчёт медианы в чётном дискретном ряду

Это означает, бальные оценки качества пищи 50 ресторанов Нью-Йорк Сити не превышают 20, а бальные оценки качества пищи других 50 ресторанов – превышают 20.

Медиана не намного больше среднего значения, равного 20,32, можно сделать вывод об отсутствии экстремальных значений, которые бы искажали смысл числовых данных.

Аналогично произведём расчёт медианы по другим критериям оценок по обеим группам. Результаты вычислений занесём в таблицы 1 и 2. Тот же вывод об отсутствии экстремальных значений можно сделать и по остальным критериям.

Мода - это величина признака наиболее часто встречающегося в совокупности.

Для оценки качества пищи в ресторанах Нью-Йорк Сити чаще всего выставлялся 21 балл, что также не сильно отличается от средней. То же можно сказать и про структурные средние стоимости обеда для одного человека.

Значения моды и медианы и округлённого до целого числа среднего значения для оценок оформления и обслуживания совпадают. Что свидетельствует о симметричном распределении.

2. Так как массив данных достаточно большой, для оценки распределения данных рассчитаем квартили, которые разбивают упорядоченный набор данных на 4 равные части.

Первый квартиль Q1 – это число, разделяющее выборку на две части: 25% данных меньше, а 75% - больше первого квартиля.

Третий квартиль Q3 – это число, разделяющее выборку на две части: 75% данных меньше, а 25% - больше третьего квартиля.

Например, первый и третий квартиль бальных оценок качества пищи 100 ресторанов Нью-Йорк Сити равны:

Q1 = 19,

Q3 = 22

соответственно.

Значения квартилей для остальных критериев указаны в таблицах 1 и 2.

3. Определим показатели вариации:

- размах,

- межквартильный размах,

- дисперсию,

- стандартное отклонение,

- коэффициент вариации каждого показателя для групп ресторанов.

Размах вариации определяется как разность между наибольшим и наименьшим значением признака:

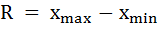
Формула размаха вариации

Так размах бальных оценок качества пищи 100 ресторанов Нью-Йорк Сити равен:

R = 27 – 14 = 13

Это означает, что разница между наибольшей и наименьшей бальной оценкой равна 13.

Результаты расчётов размаха вариации для остальных критериев занесены в таблицы 1 и 2. Общий разброс данных по критериям примерно одинаковый в обеих группах.

Межквартильный размах – это разность между третьим и первым квартилями выборки.

Межквартильный размах бальных оценок качества пищи ресторанов Нью-Йорк Сити равен

R _Q = Q3 – Q1 = 22 – 19 = 3.

Такой же размах значений и у двух других критериев.

Эта величина характеризует разброс бальных оценок качества пищи, оформления блюд и уровня обслуживания для половины ресторанов находящихся в Нью-Йорк Сити. Как видно по результатам вычислений посетители ресторанов Лонг-Айленда сильнее разобщены во мнениях, чем посетители ресторанов Нью-Йорк Сити.

Оценим степень колебания данных вокруг среднего значения с помощью дисперсии и стандартного отклонения.

Выборочная дисперсия – является приближением среднего арифметического, вычисленной на основе квадратов отклонений каждого значения признака от средней арифметической.

Для выборки из 100 бальных оценок качества пищи ресторанов Нью-Йорк Сити дисперсия будет рассчитана по формуле:

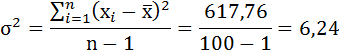
Формула и расчёт выборочной дисперсии

Теперь найдём стандартное отклонение как квадратный корень из дисперсии:

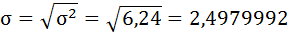
Формула и расчёт среднего квадратического отклонения

Это значит, что бальные оценки качества пищи основной массы ресторанов Нью-Йорк Сити отклоняются от среднего значения не более чем на 2,5 балла (то есть колеблются в интервале от 20,32 – 2,5 до 20,32 + 2,5).

Фактически в этом интервале лежит бальная оценка качества пищи 65% (65 из 100) от общего числа выборки ресторанов Нью-Йорк Сити.

Аналогичные вычисления выборочной дисперсии и стандартного отклонения произведём для остальных критериев обеих выборок. Результаты занесём в таблицы 1 и 2.

Вывод: Как видно из таблиц большее значение размаха, межквартильного размаха, дисперсии и стандартного отклонения имеют данные бальных оценок качества пищи, оформления блюд, уровня обслуживания группы ресторанов Лонг-Айленда, чем Нью-Йорк Сити. То есть данные об оценках группы ресторанов Лонг-Айленда имеют больший разброс, чем данные по группе ресторанов Нью-Йорк Сити. Данные по этим трём критериям по группе ресторанов Нью-Йорк Сити более плотно концентрируются вокруг своего среднего значения и более однородны, чем показатели группы ресторанов Лонг-Айленда

Однако, по такому критерию как стоимость обеда для одного человека, данные первой группы имеют больший разброс значений, чем данные второй группы.

Относительную оценку разброса определим с помощью коэффициента вариации. Он равен отношению стандартного отклонения к среднему арифметическому значению, умноженному на 100%.

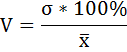
Формула коэффициента вариации

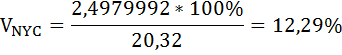
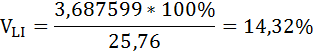
Коэффициент вариации бальных оценок качества пищи в ресторанах Нью-Йорк Сити и Лонг-Айленда равны:

Коэффициент вариации

Относительный разброс бальных оценок качества пищи в ресторанах Лонг-Айленда больше, чем в Нью-Йорк Сити.

Коэффициент вариации бальных оценок оформления в ресторанах Нью-Йорк Сити и Лонг-Айленда равны:

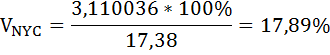
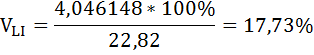
Коэффициент вариации

Относительный разброс бальных оценок оформления в ресторанах Нью-Йорк Сити больше, чем в Лонг-Айленде.

Коэффициент вариации бальных оценок обслуживания в ресторанах Нью-Йорк Сити и Лонг-Айленда равны:

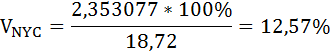
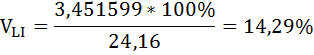
Коэффициент вариации

Относительный разброс бальных оценок обслуживания в ресторанах Лонг-Айленда больше, чем в Нью-Йорк Сити.

Коэффициент вариации суммарного рейтинга в ресторанах Нью-Йорк Сити и Лонг-Айленда равны:

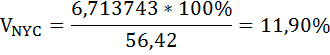
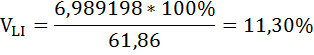
Коэффициент вариации

Относительный разброс суммарного рейтинга в ресторанах Нью-Йорк Сити больше, чем в Лонг-Айленде.

Коэффициент вариации стоимости в ресторанах Нью-Йорк Сити и Лонг-Айленда равны:

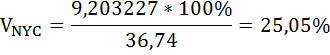
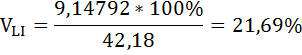
Коэффициент вариации

Относительный разброс стоимости обеда для одного человека в ресторанах Нью-Йорк Сити больше, чем в Лонг-Айленде.

4. Далее рассмотрим форму распределения выборок.

Для этого сравним среднее значение с медианой.

Среднее арифметическое бальных оценок качества пищи в ресторанах Нью-Йорк Сити равно 20,32, а медиана равна 20. Следовательно, поскольку среднее значение не на много больше медианы, распределение имеет слабую положительную асимметрию. Слабую положительную асимметрию будут также иметь распределения бальных оценок оформления и суммарный рейтинг в ресторанах Нью-Йорк Сити, а также бальных оценок обслуживания и цены в ресторанах Лонг-Айленда.

Все остальные критерии имеют слабую отрицательную асимметрию.

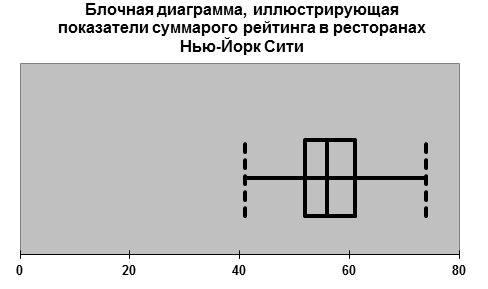
5. Построим блочные диаграммы выборок каждого показателя для групп ресторанов.

Вертикальная линия, проведённая внутри прямоугольника, отмечает медиану. Левая сторона прямоугольника соответствует первому квартилю, Q1, а правая сторона – третьему квартилю, Q3. Таким образом, прямоугольник содержит средние 50% элементов выборки. Младшие 25% данных изображаются в виде линии, соединяющей левую сторону прямоугольника с наименьшим выборочным значением xmin (левый ус). Старшим 25% соответствует линия, соединяющая правую сторону прямоугольника с наибольшим выборочным значением xmax (правый ус).

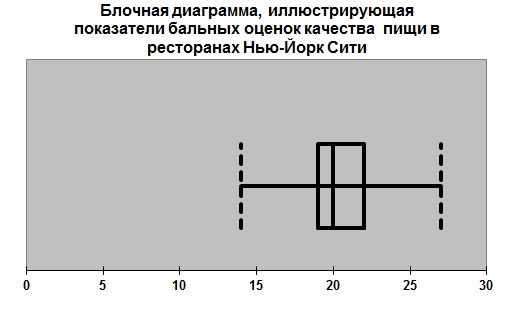
Блочная диаграмма

Диаграмма демонстрирует, практически симметричное распределение показателей бальных оценок качества пищи, поскольку расстояние между медианой и наибольшим значением равно расстоянию между наименьшим значением и медианой. Правый ус равен левому. Однако другие характеристики распределения указывают на несимметричность. Медиана расположена ближе к левой стороне диаграммы, чем к правой стороне. Однако в отличие от следующей диаграммы, на которой наблюдается симметричное распределение, здесь мы видим большую концентрацию значений бальных оценок вокруг среднего арифметического.

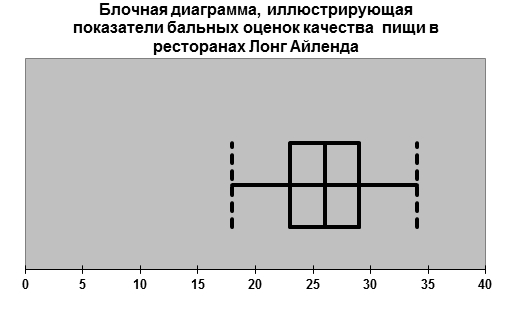
Блочная диаграмма 2

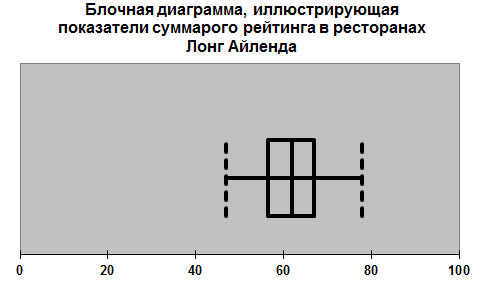
Те же выводы можно сделать при сравнении следующих двух диаграмм, иллюстрирующих показатели бальных оценок оформления.

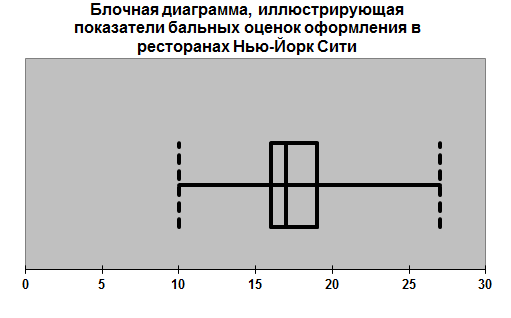
Блочная диаграмма 3

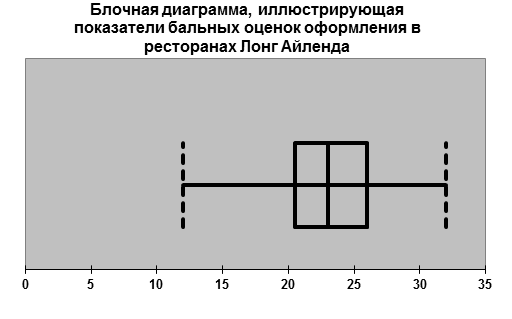
Блочная диаграмма 4

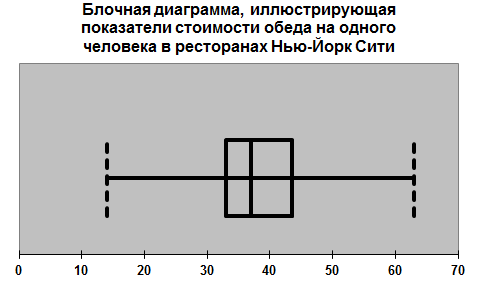
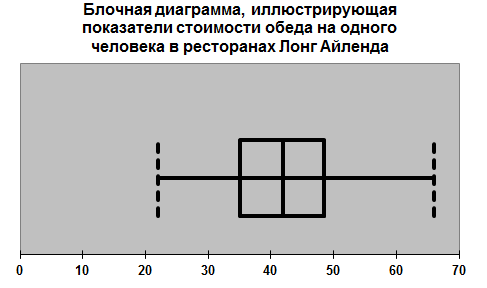
Все выводы об асимметрии распределения, сделанные выше можно проиллюстрировать на следующих блочных диаграммах.

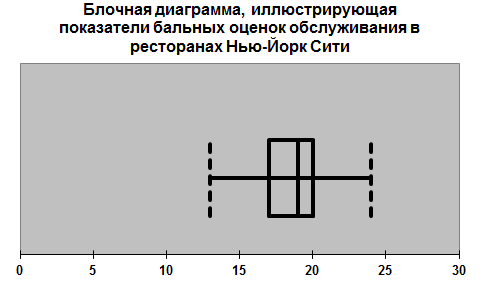
Блочная диаграмма 5

Симметрия наблюдается на следующей диаграмме, иллюстрирующей показатели бальных оценок обслуживания в ресторанах Лонг-Айленда, где расстояния от медианы до квартилей, а также до минимального и максимального значения равны.

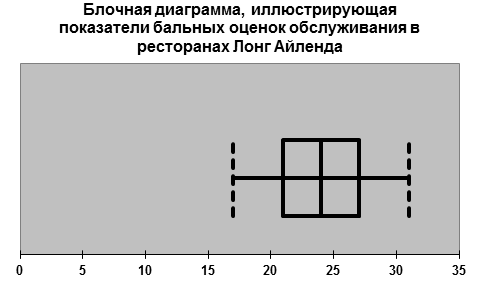
Блочная диаграмма 6

Блочная диаграмма 7

Блочная диаграмма 8

Блочная диаграмма 9

Блочная диаграмма 10

6. Найдём коэффициенты корреляции.

Коэффициент корреляции для оценки силы связи между двумя переменными – бальной оценкой качества пищи (Х) и ценой (Y):

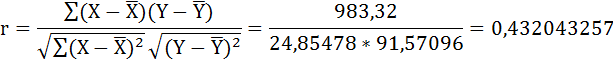
Формула и расчёт коэффициента корреляции

Между бальной оценкой качества пищи и ценой существует положительная корреляция. Связь между признаками слабая. Аналогично рассчитываются коэффициенты корреляции для остальных показателей. Результаты расчётов занесём в таблицу 3.

Таблица 3 Матрица коэффициентов парной корреляции для показателей группы ресторанов Нью-Йорк Сити
	Пища	Оформление	Обслуживание	Суммарный рейтинг	Цена
Пища	1
Оформление	0,374246938	1
Обслуживание	0,726834837	0,633045987	1
Суммарный рейтинг	0,80018237	0,824355396	0,914170432	1
Цена	0,432043257	0,584370271	0,628153654	0,65161118	1

Между бальной оценкой качества пищи и бальной оценкой оформления существует слабая положительная тенденция.

Умеренный характер связи наблюдается между бальными оценками оформления и обслуживания, между бальной оценкой оформления и стоимостью обеда на одного человека, между бальной оценкой обслуживания и стоимостью обеда на одного человека, суммарным рейтингом и стоимостью обеда на одного человека.

Сильный характер связи наблюдается между бальными оценками качества пищи и обслуживания, бальными оценками качества пищи и суммарным рейтингом, бальными оценками оформления и суммарным рейтингом, бальными оценками обслуживания и суммарным рейтингом.

В таблице 4 рассчитаны коэффициенты корреляции для показателей группы ресторанов Лонг-Айленда.

Таблица 4 Матрица коэффициентов парной корреляции для показателей группы ресторанов Лонг-Айленда
	Пища	Оформление	Обслуживание	Суммарный рейтинг	Цена
Пища	1
Оформление	0,665937147	1
Обслуживание	0,87521215	0,799854003	1
Суммарный рейтинг	0,736662379	0,793841071	0,809055286	1
Цена	0,388459639	0,528669319	0,515726531	0,651295178	1

Между всеми показателями существует положительная корреляции.

Связь между бальной оценкой качества пищи и ценой слабая.

Между бальной оценкой качества пищи и бальной оценкой оформления существующая связь носит умеренный характер.

Умеренный характер связи наблюдается между бальной оценкой оформления и стоимостью обеда на одного человека, между бальной оценкой обслуживания и стоимостью обеда на одного человека, суммарным рейтингом и стоимостью обеда на одного человека.

Сильный характер связи наблюдается между бальными оценками оформления и обслуживания, между бальными оценками качества пищи и обслуживания, бальными оценками качества пищи и суммарным рейтингом, бальными оценками оформления и суммарным рейтингом, бальными оценками обслуживания и суммарным рейтингом.

Источник данных

Условие задачи заимствовано из: Левин, Дэвид М., Стефан, Дэвид, Кребиль, Тимоти С., Беренсон, Марк Л. Статистика для менеджеров с использованием Microsoft Excel, 4-е изд.

Расчёт экономической и бухгалтерской прибыли Решение

Расчёт амортизационных отчислений Решение

	Город	Пища	Оформление	Обслуживание	Суммарный рейтинг	Цена
1	NYC	19	21	18	58	50
2	NYC	18	17	17	52	38
3	NYC	19	16	19	54	43
4	NYC	23	18	21	62	56
5	NYC	23	20	21	64	51
6	NYC	23	18	20	61	36
7	NYC	20	17	16	53	25
8	NYC	20	15	17	52	33
9	NYC	19	18	18	55	41
10	NYC	21	19	19	59	44
11	NYC	20	17	16	53	34
12	NYC	21	23	21	65	39
13	NYC	24	20	22	66	49
14	NYC	20	17	20	57	37
15	NYC	17	18	14	49	40
16	NYC	21	17	20	58	50
17	NYC	21	19	21	61	50
18	NYC	20	16	19	55	35
19	NYC	17	11	13	41	22
20	NYC	21	16	20	57	45
21	NYC	23	20	23	66	44
22	NYC	17	19	16	52	38
23	NYC	22	14	15	51	14
24	NYC	19	19	18	56	44
25	NYC	21	19	20	60	51
26	NYC	19	14	16	49	27
27	NYC	19	17	19	55	44
28	NYC	21	13	21	55	39
29	NYC	24	21	21	66	50
30	NYC	19	16	19	54	35
31	NYC	17	15	15	47	31
32	NYC	19	16	19	54	34
33	NYC	22	19	21	62	48
34	NYC	22	18	20	60	48
35	NYC	14	15	15	44	30
36	NYC	22	22	21	65	42
37	NYC	20	15	18	53	26
38	NYC	18	14	17	49	35
39	NYC	18	20	16	54	32
40	NYC	24	18	21	63	63
41	NYC	21	17	18	56	36
42	NYC	18	17	17	52	38
43	NYC	20	19	19	58	53
44	NYC	21	10	17	48	23
45	NYC	19	14	19	52	39
46	NYC	18	17	17	52	45
47	NYC	20	16	17	53	37
48	NYC	21	12	14	47	31
49	NYC	19	17	19	55	39
50	NYC	21	20	20	61	53
51	NYC	21	18	21	60	37
52	NYC	17	14	17	48	37
53	NYC	17	17	18	52	29
54	NYC	23	19	18	60	38
55	NYC	23	22	21	66	37
56	NYC	21	18	19	58	38
57	NYC	21	19	23	63	39
58	NYC	21	18	18	57	29
59	NYC	22	18	20	60	36
60	NYC	22	20	20	62	38
61	NYC	23	20	22	65	44
62	NYC	23	18	20	61	27
63	NYC	21	14	19	54	24
64	NYC	17	17	17	51	34
65	NYC	23	23	22	68	44
66	NYC	15	17	15	47	23
67	NYC	19	14	17	50	30
68	NYC	20	19	18	57	32
69	NYC	20	15	17	52	25
70	NYC	20	12	18	50	29
71	NYC	23	19	20	62	43
72	NYC	19	21	19	59	31
73	NYC	15	13	15	43	26
74	NYC	20	17	22	59	34
75	NYC	21	17	18	56	23
76	NYC	23	20	21	64	41
77	NYC	27	16	19	62	32
78	NYC	17	17	16	50	30
79	NYC	22	11	17	50	28
80	NYC	20	16	19	55	33
81	NYC	20	12	16	48	26
82	NYC	25	25	24	74	51
83	NYC	17	17	18	52	26
84	NYC	25	22	23	70	48
85	NYC	19	18	19	56	39
86	NYC	27	20	24	71	55
87	NYC	21	11	17	49	24
88	NYC	19	18	19	56	38
89	NYC	20	21	20	61	31
90	NYC	23	19	21	63	30
91	NYC	24	27	23	74	51
92	NYC	18	18	20	56	30
93	NYC	15	16	14	45	27
94	NYC	16	20	17	53	38
95	NYC	18	16	17	51	26
96	NYC	20	12	18	50	28
97	NYC	21	24	21	66	33
98	NYC	21	18	19	58	38
99	NYC	23	15	20	58	32
100	NYC	19	14	16	49	25
101	LI	22	24	21	61	53
102	LI	24	23	23	58	44
103	LI	23	20	23	58	47
104	LI	26	21	24	65	59
105	LI	30	27	28	71	58
106	LI	31	26	28	69	44
107	LI	30	27	26	63	35
108	LI	24	19	21	56	37
109	LI	24	23	23	60	46
110	LI	23	21	21	61	46
111	LI	25	22	21	58	39
112	LI	30	32	30	74	48
113	LI	29	25	27	71	54
114	LI	23	20	23	60	40
115	LI	23	24	20	55	46
116	LI	22	18	21	59	51
117	LI	26	24	26	66	55
118	LI	29	25	28	64	44
119	LI	26	20	22	50	31
120	LI	30	25	29	66	54
121	LI	31	28	31	74	52
122	LI	21	23	20	56	42
123	LI	30	22	23	59	22
124	LI	26	26	25	63	51
125	LI	24	22	23	63	54
126	LI	25	20	22	55	33
127	LI	28	26	28	64	53
128	LI	29	21	29	63	47
129	LI	31	28	28	73	57
130	LI	20	17	20	55	36
131	LI	20	18	18	50	34
132	LI	25	22	25	60	40
133	LI	25	22	24	65	51
134	LI	30	26	28	68	56
135	LI	22	23	23	52	38
136	LI	29	29	28	72	49
137	LI	28	23	26	61	34
138	LI	22	18	21	53	39
139	LI	28	30	26	64	42
140	LI	27	21	24	66	66
141	LI	29	25	26	64	44
142	LI	19	18	18	53	39
143	LI	30	29	29	68	63
144	LI	26	15	22	53	28
145	LI	22	17	22	55	42
146	LI	22	21	21	56	49
147	LI	29	25	26	62	46
148	LI	26	17	19	52	36
149	LI	28	26	28	64	48
150	LI	26	25	25	66	58
151	LI	28	25	28	67	44
152	LI	25	22	25	56	45
153	LI	26	26	27	61	38
154	LI	25	21	20	62	40
155	LI	28	27	26	71	42
156	LI	30	27	28	67	47
157	LI	26	24	28	68	44
158	LI	30	27	27	66	38
159	LI	26	22	24	64	40
160	LI	30	28	28	70	46
161	LI	31	28	30	73	52
162	LI	31	26	28	69	35
163	LI	25	18	23	58	28
164	LI	20	20	20	54	37
165	LI	25	25	24	70	46
166	LI	22	24	22	54	30
167	LI	23	18	21	54	34
168	LI	22	21	20	59	34
169	LI	30	25	27	62	35
170	LI	22	14	20	52	31
171	LI	32	28	29	71	52
172	LI	20	22	20	60	32
173	LI	19	17	19	47	30
174	LI	29	26	31	68	43
175	LI	30	26	27	65	32
176	LI	24	21	22	65	42
177	LI	34	23	26	69	39
178	LI	24	24	23	57	37
179	LI	32	21	27	60	38
180	LI	22	18	21	57	35
181	LI	23	15	19	51	29
182	LI	29	29	28	78	55
183	LI	25	25	26	60	34
184	LI	28	25	26	73	51
185	LI	27	26	27	64	47
186	LI	29	22	26	73	57
187	LI	22	12	18	50	25
188	LI	22	21	22	59	41
189	LI	24	25	24	65	35
190	LI	27	23	25	67	34
191	LI	25	28	24	75	52
192	LI	19	19	21	57	31
193	LI	18	19	17	48	30
194	LI	18	22	19	55	40
195	LI	26	24	25	59	34
196	LI	20	12	18	50	28
197	LI	25	28	25	70	37
198	LI	29	26	27	66	46
199	LI	23	15	20	58	32
200	LI	28	23	25	58	34

	Город	Пища	Оформление	Обслуживание	Суммарный рейтинг	Цена
1	NYC	19	21	18	58	50
2	NYC	18	17	17	52	38
3	NYC	19	16	19	54	43
4	NYC	23	18	21	62	56
5	NYC	23	20	21	64	51
6	NYC	23	18	20	61	36
7	NYC	20	17	16	53	25
8	NYC	20	15	17	52	33
9	NYC	19	18	18	55	41
10	NYC	21	19	19	59	44
11	NYC	20	17	16	53	34
12	NYC	21	23	21	65	39
13	NYC	24	20	22	66	49
14	NYC	20	17	20	57	37
15	NYC	17	18	14	49	40
16	NYC	21	17	20	58	50
17	NYC	21	19	21	61	50
18	NYC	20	16	19	55	35
19	NYC	17	11	13	41	22
20	NYC	21	16	20	57	45
21	NYC	23	20	23	66	44
22	NYC	17	19	16	52	38
23	NYC	22	14	15	51	14
24	NYC	19	19	18	56	44
25	NYC	21	19	20	60	51
26	NYC	19	14	16	49	27
27	NYC	19	17	19	55	44
28	NYC	21	13	21	55	39
29	NYC	24	21	21	66	50
30	NYC	19	16	19	54	35
31	NYC	17	15	15	47	31
32	NYC	19	16	19	54	34
33	NYC	22	19	21	62	48
34	NYC	22	18	20	60	48
35	NYC	14	15	15	44	30
36	NYC	22	22	21	65	42
37	NYC	20	15	18	53	26
38	NYC	18	14	17	49	35
39	NYC	18	20	16	54	32
40	NYC	24	18	21	63	63
41	NYC	21	17	18	56	36
42	NYC	18	17	17	52	38
43	NYC	20	19	19	58	53
44	NYC	21	10	17	48	23
45	NYC	19	14	19	52	39
46	NYC	18	17	17	52	45
47	NYC	20	16	17	53	37
48	NYC	21	12	14	47	31
49	NYC	19	17	19	55	39
50	NYC	21	20	20	61	53
51	NYC	21	18	21	60	37
52	NYC	17	14	17	48	37
53	NYC	17	17	18	52	29
54	NYC	23	19	18	60	38
55	NYC	23	22	21	66	37
56	NYC	21	18	19	58	38
57	NYC	21	19	23	63	39
58	NYC	21	18	18	57	29
59	NYC	22	18	20	60	36
60	NYC	22	20	20	62	38
61	NYC	23	20	22	65	44
62	NYC	23	18	20	61	27
63	NYC	21	14	19	54	24
64	NYC	17	17	17	51	34
65	NYC	23	23	22	68	44
66	NYC	15	17	15	47	23
67	NYC	19	14	17	50	30
68	NYC	20	19	18	57	32
69	NYC	20	15	17	52	25
70	NYC	20	12	18	50	29
71	NYC	23	19	20	62	43
72	NYC	19	21	19	59	31
73	NYC	15	13	15	43	26
74	NYC	20	17	22	59	34
75	NYC	21	17	18	56	23
76	NYC	23	20	21	64	41
77	NYC	27	16	19	62	32
78	NYC	17	17	16	50	30
79	NYC	22	11	17	50	28
80	NYC	20	16	19	55	33
81	NYC	20	12	16	48	26
82	NYC	25	25	24	74	51
83	NYC	17	17	18	52	26
84	NYC	25	22	23	70	48
85	NYC	19	18	19	56	39
86	NYC	27	20	24	71	55
87	NYC	21	11	17	49	24
88	NYC	19	18	19	56	38
89	NYC	20	21	20	61	31
90	NYC	23	19	21	63	30
91	NYC	24	27	23	74	51
92	NYC	18	18	20	56	30
93	NYC	15	16	14	45	27
94	NYC	16	20	17	53	38
95	NYC	18	16	17	51	26
96	NYC	20	12	18	50	28
97	NYC	21	24	21	66	33
98	NYC	21	18	19	58	38
99	NYC	23	15	20	58	32
100	NYC	19	14	16	49	25
101	LI	22	24	21	61	53
102	LI	24	23	23	58	44
103	LI	23	20	23	58	47
104	LI	26	21	24	65	59
105	LI	30	27	28	71	58
106	LI	31	26	28	69	44
107	LI	30	27	26	63	35
108	LI	24	19	21	56	37
109	LI	24	23	23	60	46
110	LI	23	21	21	61	46
111	LI	25	22	21	58	39
112	LI	30	32	30	74	48
113	LI	29	25	27	71	54
114	LI	23	20	23	60	40
115	LI	23	24	20	55	46
116	LI	22	18	21	59	51
117	LI	26	24	26	66	55
118	LI	29	25	28	64	44
119	LI	26	20	22	50	31
120	LI	30	25	29	66	54
121	LI	31	28	31	74	52
122	LI	21	23	20	56	42
123	LI	30	22	23	59	22
124	LI	26	26	25	63	51
125	LI	24	22	23	63	54
126	LI	25	20	22	55	33
127	LI	28	26	28	64	53
128	LI	29	21	29	63	47
129	LI	31	28	28	73	57
130	LI	20	17	20	55	36
131	LI	20	18	18	50	34
132	LI	25	22	25	60	40
133	LI	25	22	24	65	51
134	LI	30	26	28	68	56
135	LI	22	23	23	52	38
136	LI	29	29	28	72	49
137	LI	28	23	26	61	34
138	LI	22	18	21	53	39
139	LI	28	30	26	64	42
140	LI	27	21	24	66	66
141	LI	29	25	26	64	44
142	LI	19	18	18	53	39
143	LI	30	29	29	68	63
144	LI	26	15	22	53	28
145	LI	22	17	22	55	42
146	LI	22	21	21	56	49
147	LI	29	25	26	62	46
148	LI	26	17	19	52	36
149	LI	28	26	28	64	48
150	LI	26	25	25	66	58
151	LI	28	25	28	67	44
152	LI	25	22	25	56	45
153	LI	26	26	27	61	38
154	LI	25	21	20	62	40
155	LI	28	27	26	71	42
156	LI	30	27	28	67	47
157	LI	26	24	28	68	44
158	LI	30	27	27	66	38
159	LI	26	22	24	64	40
160	LI	30	28	28	70	46
161	LI	31	28	30	73	52
162	LI	31	26	28	69	35
163	LI	25	18	23	58	28
164	LI	20	20	20	54	37
165	LI	25	25	24	70	46
166	LI	22	24	22	54	30
167	LI	23	18	21	54	34
168	LI	22	21	20	59	34
169	LI	30	25	27	62	35
170	LI	22	14	20	52	31
171	LI	32	28	29	71	52
172	LI	20	22	20	60	32
173	LI	19	17	19	47	30
174	LI	29	26	31	68	43
175	LI	30	26	27	65	32
176	LI	24	21	22	65	42
177	LI	34	23	26	69	39
178	LI	24	24	23	57	37
179	LI	32	21	27	60	38
180	LI	22	18	21	57	35
181	LI	23	15	19	51	29
182	LI	29	29	28	78	55
183	LI	25	25	26	60	34
184	LI	28	25	26	73	51
185	LI	27	26	27	64	47
186	LI	29	22	26	73	57
187	LI	22	12	18	50	25
188	LI	22	21	22	59	41
189	LI	24	25	24	65	35
190	LI	27	23	25	67	34
191	LI	25	28	24	75	52
192	LI	19	19	21	57	31
193	LI	18	19	17	48	30
194	LI	18	22	19	55	40
195	LI	26	24	25	59	34
196	LI	20	12	18	50	28
197	LI	25	28	25	70	37
198	LI	29	26	27	66	46
199	LI	23	15	20	58	32
200	LI	28	23	25	58	34

Задача №43. Расчёт описательных статистик

Решение:

Экономическая прибыль

Есть график!

Счёт операций с капиталом

ВНД, ВРП, ВНС

Счёт использования располагаемого дохода

Счёт производства

Смотри ещё

Рыночное рановесие

Рыночное равновесие

Рыночное равновесие

Эластичность

ВВП

	Город	Пища	Оформление	Обслуживание	Суммарный рейтинг	Цена
1	NYC	19	21	18	58	50
2	NYC	18	17	17	52	38
3	NYC	19	16	19	54	43
4	NYC	23	18	21	62	56
5	NYC	23	20	21	64	51
6	NYC	23	18	20	61	36
7	NYC	20	17	16	53	25
8	NYC	20	15	17	52	33
9	NYC	19	18	18	55	41
10	NYC	21	19	19	59	44
11	NYC	20	17	16	53	34
12	NYC	21	23	21	65	39
13	NYC	24	20	22	66	49
14	NYC	20	17	20	57	37
15	NYC	17	18	14	49	40
16	NYC	21	17	20	58	50
17	NYC	21	19	21	61	50
18	NYC	20	16	19	55	35
19	NYC	17	11	13	41	22
20	NYC	21	16	20	57	45
21	NYC	23	20	23	66	44
22	NYC	17	19	16	52	38
23	NYC	22	14	15	51	14
24	NYC	19	19	18	56	44
25	NYC	21	19	20	60	51
26	NYC	19	14	16	49	27
27	NYC	19	17	19	55	44
28	NYC	21	13	21	55	39
29	NYC	24	21	21	66	50
30	NYC	19	16	19	54	35
31	NYC	17	15	15	47	31
32	NYC	19	16	19	54	34
33	NYC	22	19	21	62	48
34	NYC	22	18	20	60	48
35	NYC	14	15	15	44	30
36	NYC	22	22	21	65	42
37	NYC	20	15	18	53	26
38	NYC	18	14	17	49	35
39	NYC	18	20	16	54	32
40	NYC	24	18	21	63	63
41	NYC	21	17	18	56	36
42	NYC	18	17	17	52	38
43	NYC	20	19	19	58	53
44	NYC	21	10	17	48	23
45	NYC	19	14	19	52	39
46	NYC	18	17	17	52	45
47	NYC	20	16	17	53	37
48	NYC	21	12	14	47	31
49	NYC	19	17	19	55	39
50	NYC	21	20	20	61	53
51	NYC	21	18	21	60	37
52	NYC	17	14	17	48	37
53	NYC	17	17	18	52	29
54	NYC	23	19	18	60	38
55	NYC	23	22	21	66	37
56	NYC	21	18	19	58	38
57	NYC	21	19	23	63	39
58	NYC	21	18	18	57	29
59	NYC	22	18	20	60	36
60	NYC	22	20	20	62	38
61	NYC	23	20	22	65	44
62	NYC	23	18	20	61	27
63	NYC	21	14	19	54	24
64	NYC	17	17	17	51	34
65	NYC	23	23	22	68	44
66	NYC	15	17	15	47	23
67	NYC	19	14	17	50	30
68	NYC	20	19	18	57	32
69	NYC	20	15	17	52	25
70	NYC	20	12	18	50	29
71	NYC	23	19	20	62	43
72	NYC	19	21	19	59	31
73	NYC	15	13	15	43	26
74	NYC	20	17	22	59	34
75	NYC	21	17	18	56	23
76	NYC	23	20	21	64	41
77	NYC	27	16	19	62	32
78	NYC	17	17	16	50	30
79	NYC	22	11	17	50	28
80	NYC	20	16	19	55	33
81	NYC	20	12	16	48	26
82	NYC	25	25	24	74	51
83	NYC	17	17	18	52	26
84	NYC	25	22	23	70	48
85	NYC	19	18	19	56	39
86	NYC	27	20	24	71	55
87	NYC	21	11	17	49	24
88	NYC	19	18	19	56	38
89	NYC	20	21	20	61	31
90	NYC	23	19	21	63	30
91	NYC	24	27	23	74	51
92	NYC	18	18	20	56	30
93	NYC	15	16	14	45	27
94	NYC	16	20	17	53	38
95	NYC	18	16	17	51	26
96	NYC	20	12	18	50	28
97	NYC	21	24	21	66	33
98	NYC	21	18	19	58	38
99	NYC	23	15	20	58	32
100	NYC	19	14	16	49	25
101	LI	22	24	21	61	53
102	LI	24	23	23	58	44
103	LI	23	20	23	58	47
104	LI	26	21	24	65	59
105	LI	30	27	28	71	58
106	LI	31	26	28	69	44
107	LI	30	27	26	63	35
108	LI	24	19	21	56	37
109	LI	24	23	23	60	46
110	LI	23	21	21	61	46
111	LI	25	22	21	58	39
112	LI	30	32	30	74	48
113	LI	29	25	27	71	54
114	LI	23	20	23	60	40
115	LI	23	24	20	55	46
116	LI	22	18	21	59	51
117	LI	26	24	26	66	55
118	LI	29	25	28	64	44
119	LI	26	20	22	50	31
120	LI	30	25	29	66	54
121	LI	31	28	31	74	52
122	LI	21	23	20	56	42
123	LI	30	22	23	59	22
124	LI	26	26	25	63	51
125	LI	24	22	23	63	54
126	LI	25	20	22	55	33
127	LI	28	26	28	64	53
128	LI	29	21	29	63	47
129	LI	31	28	28	73	57
130	LI	20	17	20	55	36
131	LI	20	18	18	50	34
132	LI	25	22	25	60	40
133	LI	25	22	24	65	51
134	LI	30	26	28	68	56
135	LI	22	23	23	52	38
136	LI	29	29	28	72	49
137	LI	28	23	26	61	34
138	LI	22	18	21	53	39
139	LI	28	30	26	64	42
140	LI	27	21	24	66	66
141	LI	29	25	26	64	44
142	LI	19	18	18	53	39
143	LI	30	29	29	68	63
144	LI	26	15	22	53	28
145	LI	22	17	22	55	42
146	LI	22	21	21	56	49
147	LI	29	25	26	62	46
148	LI	26	17	19	52	36
149	LI	28	26	28	64	48
150	LI	26	25	25	66	58
151	LI	28	25	28	67	44
152	LI	25	22	25	56	45
153	LI	26	26	27	61	38
154	LI	25	21	20	62	40
155	LI	28	27	26	71	42
156	LI	30	27	28	67	47
157	LI	26	24	28	68	44
158	LI	30	27	27	66	38
159	LI	26	22	24	64	40
160	LI	30	28	28	70	46
161	LI	31	28	30	73	52
162	LI	31	26	28	69	35
163	LI	25	18	23	58	28
164	LI	20	20	20	54	37
165	LI	25	25	24	70	46
166	LI	22	24	22	54	30
167	LI	23	18	21	54	34
168	LI	22	21	20	59	34
169	LI	30	25	27	62	35
170	LI	22	14	20	52	31
171	LI	32	28	29	71	52
172	LI	20	22	20	60	32
173	LI	19	17	19	47	30
174	LI	29	26	31	68	43
175	LI	30	26	27	65	32
176	LI	24	21	22	65	42
177	LI	34	23	26	69	39
178	LI	24	24	23	57	37
179	LI	32	21	27	60	38
180	LI	22	18	21	57	35
181	LI	23	15	19	51	29
182	LI	29	29	28	78	55
183	LI	25	25	26	60	34
184	LI	28	25	26	73	51
185	LI	27	26	27	64	47
186	LI	29	22	26	73	57
187	LI	22	12	18	50	25
188	LI	22	21	22	59	41
189	LI	24	25	24	65	35
190	LI	27	23	25	67	34
191	LI	25	28	24	75	52
192	LI	19	19	21	57	31
193	LI	18	19	17	48	30
194	LI	18	22	19	55	40
195	LI	26	24	25	59	34
196	LI	20	12	18	50	28
197	LI	25	28	25	70	37
198	LI	29	26	27	66	46
199	LI	23	15	20	58	32
200	LI	28	23	25	58	34