Задача №137. Расчёт объёмов продаж и цены в случае ценовой дискриминации

Даны функция затрат монополии

TC = 500 + 12 × Q + 0,5 × Q²

и функция спроса на продукцию этой монополии на двух рынках:

Q₁ = 400 - 2 × P₁,

Q₂ = 1250 - 5 × P₂.

Других рынков сбыта нет. Найти объёмы продаж и цены на каждом из двух рынков, при которых суммарная прибыль монополии будет максимальной.

Решение:

Найдём обратные функции спроса:

P₁ = 200 - 0,5 × Q₁,

P₂ = 250 - 0,2 × Q₂.

Тогда общий доход на каждом из двух сегментов рынка будет равен:

TR₁ = 200 × Q₁ - 0,5 × Q2_1,

TR₂ = 250 × Q₂ - 0,2 × Q²_2.

Следовательно, предельный доход на первом сегменте рынка равен:

MR₁ = (TR₁)' = 200 - Q₁

На втором:

MR₂ = (TR₂)' = 250 - 0,4 × Q₂

Рассчитаем предельные затраты:

МС = ТС' = (500 + 12 × Q + 0,5 × Q²)' = 12 + Q,

где

Q = Q₁ + Q₂

Предельный доход на каждом сегменте рынка равен общерыночным предельным издержкам. Составим систему из двух уравнений с двумя неизвестными:

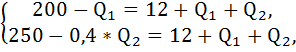
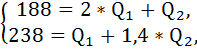
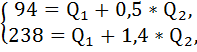
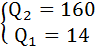
Подставим значения объёма в обратные функции спроса, получим цены на каждом сегменте рынка:

P₁ = 200 - 0,5 × 14 = 193,

P₂ = 250 - 0,2 × 160 = 218.

Определим общую прибыль как сумму прибылей на каждом рыночном сегменте:

П = TR₁ + TR₂ - TC =

 = Q₁ × P₁ + Q₂ × P₂ - (500 + 12 × (Q₁ + Q₂) + 0,5 × (Q₁ + Q₂)²) =

 = 14 × 193 + 160 × 218 - (500 + 12 × 174 + 0,5 × 1742) = 19 856