Задача №196. Расчёт оптимума производства
Рыболовное судно может войти в порт и покинуть его только во время прилива с 6 до 7 часов. На практике судно располагает 24 часами на путь до места лова и обратно и собственно ловли рыбы. Зона лова находится в 30 милях от порта. Чем быстрее судно туда доберется, тем больше времени оно сможет потратить на саму ловлю. В тоже время расход топлива зависит от скорости:
| Скорость (миль/час) | Расход топлива (галлонов на 60 миль) |
|---|---|
| 6 | 10 |
| 7 | 11 |
| 8 | 13 |
| 9 | 16 |
| 10 | 20 |
| 11 | 25 |
| 12 | 31 |
| 13 | 38 |
Во время ловли топливо не расходуется. Цена топлива равна $1 за галлон. Все прочие расходы от скорости не зависят. Каждый час лова позволяет добыть рыбу, стоимостью $10. Какую скорость должно выбрать судно, если его владелец хочет максимизировать прибыль? Ответ обоснуйте, сделав расчёт двумя способами.
Решение:

а) Способ 1. Сопоставление валового дохода и валовых издержек:
Определим величину валового дохода по формуле:
TR = Q × P,
где
TR – валовой (общий) доход от продажи рыбы,
Q – выпуск или количество произведённого товара (в данном кейсе количество часов лова),
Представим время лова функцией, зависящей от скорости (υ) судна:
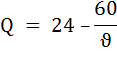
Р – цена товара (в данном кейсе стоимость рыбы, пойманной за час, то есть $10).
Тогда функция выручки будет иметь вид:
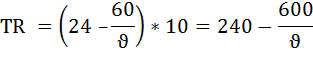
Валовые (общие) издержки TC, состоят только из расходов на топливо.
ТС = Расход топлива × Ртоплива,
где
Ртоплива – цена топлива.
Так, например, при скорости судна 6 миль/ч общий доход будет равен:
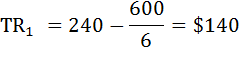
а величина валовых затрат:
TC1 = 10 × 1 = $10
Аналогично производится расчёт валового дохода и валовых издержек при остальных значениях скорости.
Результаты вычислений занесём в таблицу.
| Скорость (миль/час) | Расход топлива (галлонов на 60 миль) | TC,$ | TR,$ | TR – TC, $ |
|---|---|---|---|---|
| 6 | 10 | 10 | 140,00 | 130,00 |
| 7 | 11 | 11 | 154,29 | 143,29 |
| 8 | 13 | 13 | 165,00 | 152,00 |
| 9 | 16 | 16 | 173,33 | 157,33 |
| 10 | 20 | 20 | 180,00 | 160,00 |
| 11 | 25 | 25 | 185,45 | 160,45 |
| 12 | 31 | 31 | 190,00 | 159,00 |
| 13 | 38 | 38 | 193,85 | 155,85 |
Сопоставив валовой доход и валовые издержки, приходим к выводу, что прибыль
П = TR – TC
будет максимальной при скорости судна 11 миль/ч.
б) Способ 2. Сопоставление предельного дохода и предельных издержек.
Предприятие (в данном случае владелец судна), которое стремится к максимуму прибыли, выберет такой объём производства, при котором предельные затраты будут равны предельному доходу.
То есть когда выполняется равенство:
MС = MR.
Предельные затраты (МС) – это прирост общих затрат, связанный с ростом выпуска продукции на дополнительную единицу.
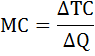
Предельная выручка (MR) – это прирост выручки, связанный с ростом выпуска продукции на дополнительную единицу.
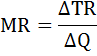
Предельная прибыль (Мπ) – это прирост общей прибыли, связанный с производством дополнительной единицы продукции. Предельную прибыль можно найти также как разность предельной выручки и предельных затрат:
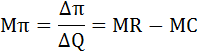
Правило принятия решения об объёме производства гласит: пока предельная прибыль положительна, предприятию следует наращивать объём производства. В данном кейсе переформулируем: пока предельная прибыль положительна, судну следует наращивать время ловли, а следовательно, увеличивать скорость движения к месту ловли.
Рассчитаем величину времени лова, предельных затрат, предельной выручки и предельной прибыли.
При скорости υ = 6 миль/час время лова будет равно:
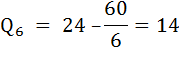
При скорости υ = 7 миль/час время лова будет равно:
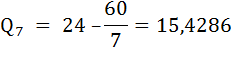
Предельные издержки:
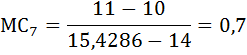
Предельная выручка:
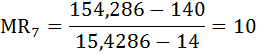
Предельная прибыль:
Мπ7 = MR7 – MC7 = 10 – 0,7 = 9,3
Результаты остальных вычислений занесём в таблицу.
| Скорость (миль/час) | Q | TC,$ | TR,$ | MC, $ | MR, $ | Мπ = MR – MC, $ |
|---|---|---|---|---|---|---|
| 6 | 14 | 10 | 140,00 | - | - | - |
| 7 | 15,4286 | 11 | 154,29 | 0,7 | 10 | 9.3 |
| 8 | 16,5 | 13 | 165,00 | 1,8667 | 10 | 8,1333 |
| 9 | 17,3333 | 16 | 173,33 | 3,6 | 10 | 6,4 |
| 10 | 18 | 20 | 180,00 | 6 | 10 | 4 |
| 11 | 18,5455 | 25 | 185,45 | 9,1667 | 10 | 0,8333 |
| 12 | 19 | 31 | 190,00 | 13,2 | 10 | -3,2 |
| 13 | 19,3846 | 38 | 193,85 | 18,2 | 10 | -8,2 |
Из таблицы видно, что предельная прибыль положительна при Q =18,55 и при скорости движения υ = 11 миль/час, а вот уже при Q = 19 торопиться не стоит, так как предельная прибыль уже приняла отрицательное значение. Следовательно, скорость, которую должно выбрать судно, если его владелец хочет максимизировать прибыль должна быть 11 миль/час.

Рыночное равновесие
Смотри ещё
- Анализ рыночной структуры / Задача №151. Расчёт равновесного объема и монопольной цены
- Анализ рыночной структуры / Задача № 152. Расчёт оптимального объёма выпуска, цены и прибыли монополиста
- Анализ рыночной структуры / Задача №153. Расчёт индекса Лернера
- Анализ рыночной структуры / Задача №154. Расчёт равновесной цены, объёма выпуска и прибыли
- Анализ рыночной структуры / Задача №155. Расчёт объема продаж, цены и прибыли фирмы монополистического конкурента
- Анализ рыночной структуры / Задача №156. Расчёт рыночной цены и оптимальный объём выпуска
- Анализ рыночной структуры / Задача №157. Расчёт оптимального выпуска и цены фирмы монополиста
- Анализ рыночной структуры / Задача №158. Расчёт избыточной мощности фирмы
- Анализ рыночной структуры / Задача №159. Расчёт оптимального выпуска и цены до и после рекламной кампании
- Анализ рыночной структуры / Задача №168. Расчёт объема выпуска продукции
- Анализ рыночной структуры / Задача №174. Расчёт параметров равновесия на рынке монополистической конкуренции
- Анализ рыночной структуры / Задача №183. Расчёт индекса Лернера
- Анализ рыночной структуры / Задача №188. Расчёт параметров рыночного равновесия по Курно
- Анализ рыночной структуры / Задача №189. Расчёт избыточной производственной мощности
- Анализ рыночной структуры / Задача №197. Расчёт выпуска и цены лидера
- Анализ рыночной структуры / Задача №198. Лидерство в ценообразовании
- Анализ рыночной структуры / Задача №199. Расчёт ущерба от монополии
- Основные макроэкономические показатели / Задача №26. Расчёт ВВП по доходам
- Провалы рынка и государственное регулирование / Задача №194. Расчёт общественно оптимального уровня производства фирмы
- Производство и затраты фирмы / Задача №71. Расчёт затрат
- Производство и затраты фирмы / Задача №72. Расчёт затрат
- Производство и затраты фирмы / Задача №73. Расчёт бухгалтерской и экономической прибыли
- Производство и затраты фирмы / Задача №74. Расчёт бухгалтерской и экономической прибыли
- Производство и затраты фирмы / Задача №75. Расчёт амортизационных отчислений, бухгалтерских и экономических издержек, прибыли
- Производство и затраты фирмы / Задача №76. Расчёт величины годовых бухгалтерских и экономических издержек, экономической и бухгалтерской прибыли
- Производство и затраты фирмы / Задача №77. Расчёт бухгалтерской и экономической прибыли и ставки налога на прибыль
- Производство и затраты фирмы / Задача №78. Расчёт амортизационных отчислений, бухгалтерских и экономических издержек и прибыли
- Производство и затраты фирмы / Задача №79. Определение функций постоянных, переменных, предельных и средних издержек
- Производство и затраты фирмы / Задача №80. Определение функций общих и предельных затрат
- Производство и затраты фирмы / Задача №81. Расчёт минимума функции средних общих затрат






















