Задача №188. Расчёт параметров рыночного равновесия по Курно

На рынке действуют две фирмы. Функция издержек для фирмы 1:

ТС(q₁) = 2 × q_1,

_{и для фирмы 2:}

ТС(q₂) = q₂²

Обратная функция рыночного спроса описывается уравнением:

P(Q) = 250 – 4 × Q,

где

Q = q₁ + q₂.

а) Определите объёмы выпуска фирм в равновесии Курно, максимизирующие их прибыли. Какой в этом случае будет рыночная цена? Какую прибыль получит каждая фирма?

б) Определите параметры рыночного равновесия по Штакельбергу. Какую прибыль получит каждая фирма?

в) Какая установится цена в соответствии с картельным соглашением?

 

Решение:

а) Подставим общий выпуск двух фирм

Q = q₁ + q₂

в формулу отраслевого спроса, получим:

P(Q) = 250 – 4 × (q₁ + q₂)

Распишем прибыли олигополистов:

П₁ = TR₁ – TC₁ = P × q₁ – 2 × q₁ = (250 – 4 × (q₁ + q₂)) × q₁ – 2 × q₁ =

= 250 × q₁ – 4 × q₁2 – 4 × q₁ × q₂ – 2 × q₁ =

=248 × q₁ – 4 × q₁² – 4 × q₁ × q₂

П₂ = TR₂ – TC₂ = P × q₂ – q₂² = (250 – 4 × (q₁ + q₂)) × q₂ – q₂² =

 = 250 × q₂ – 4 × q₂² – 4 × q₁ × q₂ – q₂² =

 =250 × q₂ – 5 × q₂² – 4 × q₁ × q₂

Каждая фирма стремится к максимуму прибыли.

Найдём максимум функций прибыли. Для этого приравняем к нулю первые производные полученных функций и найдём оптимальный объём выпуска:

П₁' = 248 – 8 × q₁ – 4 × q₂ = 0

П₂' = 250 – 10 × q₂ – 4 × q₁= 0

Уравнение реакции для 1 фирмы: q₁ = 31 – 0,5 × q₂ 

Уравнение реакции для 2 фирмы: q₂ = 25 – 0,4 × q₁

Точка пересечения этих линий определяет рыночное равновесие для монополистов.

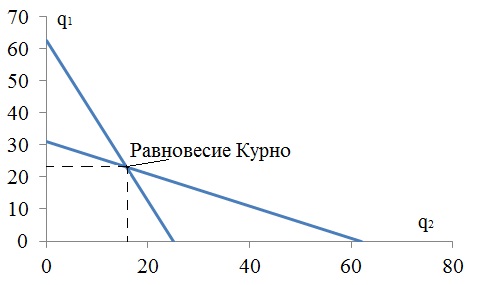
Решив систему из двух уравнений реакции дуополистов, получим равновесные значения выпуска для первой и второй фирмы.

q*₁ = 23,125

q*₂ = 15,75

Подставив равновесные значения q*₁ и q*₂ в функцию отраслевого спроса

P(Q) = 250 – 4 × (q₁ + q₂),

найдём цену равновесия.

Р = 250 – 4 × 23,125 – 4 × 15,75 = 94,5

Рассчитаем прибыль каждой фирмы в отдельности:

П₁ = 94,5 × 23,125 – 2 × 23,125 = 2139,06

П₂ = 94,5 × 15,75 – 15,75² = 1240,31

б) Пусть фирма 1 выступает в роли лидера, а фирма 2 - в роли последователя.

Тогда прибыль первой фирмы с учётом уравнения реакции фирмы 2 будет равна:

П₁ = 248 × q₁ – 4 × q₁² – 4 × q₁ × (25 – 0,4 × q₁) = 148 × q₁ – 2,4 × q₁²

Она достигает максимума при

П₁' = 0

148 – 4,8 × q₁ = 0

q₁ = 30,83

При этом выпуск второй фирмы станет равным:

q₂ = 25 – 0,4 × 30,83 = 12,668,

Р = 250 - 4 × 30,83 - 4 × 12,67 = 76,

П₁ = 76 × 30,83 - 2 × 30,83 = 2281,42,

П₂ = 76 × 12,67 - 12,672 = 802,39.

Таким образом, в результате пассивного поведения фирмы 2 её прибыль снизилась, а фирмы 1 возросла.

В случае лидерства фирмы 2 её прибыль будет равна:

П₂ = 250 × q₂ – 5 × q₂² – 4 × (31 – 0,5 × q₂ ) × q₂ = 126 × q₂ – 3 × q₂²

Определим производную этой функции и приравняем её к нулю.

П₂' = 0

126 – 6 × q₂ = 0

q₂ = 21

q₁ = 31 – 0,5 × 21 = 20,5

Р = 250 - 4 × 20,5 - 4 × 21 = 84

П₁ = 84 × 20,5 - 2 × 20,5 = 1681

П₂ = 84 × 21 - 21² = 1323.

Таким образом, в результате пассивного поведения фирмы 1 её прибыль снизилась, а фирмы 2 возросла.

в) Если обе фирмы объединятся в картель, то их общая прибыль будет определяться по формуле:
Пk = TRk – TCk = (250 – 4 × q₁ – 4 × q₂) × (q₁ + q₂) – 2 × q₁ – q₂² =

= 248 × q₁ – 4 × q₁2 – 8 × q₁ × q₂ + 250 × q₂ – 5 × q₂²

Рассчитаем частные производные прибыли по аргументу q₁  и по аргументу q₂:

П_q1' = 248 – 8 × q₁ – 8 × q₂ = 0,

П_q2' = – 8 × q₁ + 250 – 10 × q₂ = 0.

Решим эту систему уравнений. Вычтем из второго уравнения первое и получим:

2 – 2 × q₂ = 0.

q₂ = 1,

q₁ = 30,

Q = 31,

P = 250 – 4 × 31 = 126,

Прибыль картеля при этом:

Пk =  (250 – 4 × 30 – 4 × 1) × 31 – 2 × 30 – 1² = 3 845