Задача №127. Расчёт прибыли, оптимальной цены и выпуска продукции

Допустим, общие затраты монополии равны

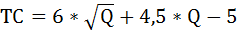
при спросе на её продукцию

Q = 32 – 4 × Р.

Найти оптимальную цену и выпуск продукции, обеспечивающие наибольшую прибыль. Вычислить эту прибыль.

Решение:

Оптимальный выпуск продукции найдём с помощью условия максимизации прибыли:

МС = MR

Найдём функции предельных издержек и предельного дохода.

Продифференцируем функцию общих издержек и определим функцию предельных издержек.

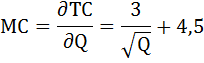
Для определения функции предельного дохода найдём функцию общего дохода по формуле:

TR = P × Q

P выразим из функции спроса, получим обратную функцию спроса. Подставим её в формулу общего дохода:

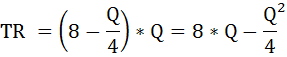
Найдём производную этой функции и получим функцию предельного дохода.

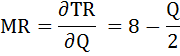
Теперь можно составить уравнение:

МС = MR.

Надо отметить, что это необходимое, но не достаточное условие максимизации прибыли.

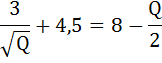
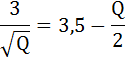
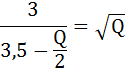
Возведём обе части в квадрат:

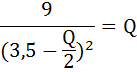
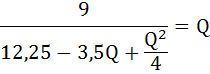
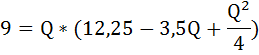
Умножим обе части уравнения на - 4 и перенесём все слагаемые в левую часть уравнения:

Q³ – 14 × Q² + 49 × Q – 36 = 0

Найдём корни этого кубического уравнения:
(Q² – 10 × Q + 9)(Q – 4) = 0

Корни квадратного уравнения 9 и 1.

Таким образом, получено 3 корня:

Q₁ = 4, Q₂ = 9, Q₃ = 1.

Как уже было отмечено МС = MR – это необходимое, но не достаточное условие максимизации прибыли. В этом можно убедиться, определив величину прибыли в каждом из трёх случаев:

при Q₁ = 4, P₁ = 8 – 1 = 7

П₁ = TR₁ – TC₁ = P₁ * Q₁ – TC₁ = 7 * 4 – 6 * 2 – 4,5 * 4 + 5 = 3;

при Q₂ = 9, P₂ = 8 – 2,25 = 5,7

П₂ = TR₂ – TC₂ = P₂ * Q₂ – TC₂ = 5,75 * 9 – 6 * 3 – 4,5 * 9 + 5 = – 1,75;

при Q₃ = 1, P₃ = 8 – 0,25 = 7,75

П₃ = TR₃ – TC₃ = P₃ * Q₃ – TC₃ = 7,75 * 1 – 6 * 1 – 4,5 * 1 + 5 = 2,25

Итак, максимум прибыли достигается при Q₁ = 4 и P₁ = 7.