Задача №123. Расчёт фиксированных затрат

Известна функция спроса на продукцию монополиста

Q = 220 - 4 × P,

и дана функция предельных затрат

MC = 10 + 4 × Q.

Известно, что максимум прибыли монополиста равен 125. Найти его фиксированные затраты.

Решение:

Известна прямая функция спроса на продукцию монополиста

Q = 220 - 4 × P.

Найдём обратную функцию спроса:

Р = 55 - 0,25 × Q.

Функция общего дохода монополиста будет иметь вид:

TR = P × Q = (55 - 0,25 × Q) × Q = 55 × Q - 0,25 × Q²

Продифференцируем функцию общего дохода и получим предельный доход:

MR = TR' = (55 × Q - 0,25 × Q²)' = 55 - 0,5 × Q

Воспользуемся условием максимизации прибыли монополии и найдём оптимальный объём производства:

MC = MR

10 + 4 × Q = 55 - 0,5 × Q

4,5 × Q = 45

Q = 10 - оптимальный объём производства монополиста.

Который будет продан по цене:

Р = 55 - 0,25 × 10 = 52,5.

Таким образом, доход от продаж составит:

TR = P × Q = 52,5 × 10 = 525

По условию задачи прибыль равна 125. Это величина общего дохода за вычетом общих издержек:

П = TR - TC = 525 - TC = 125.

Отсюда величина общих издержек равна:

ТС = 525 - 125 = 400

В то же время функция общих издержек равна первообразной от функции предельных издержек:

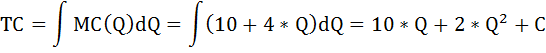
 где

С - константа, не зависящая от Q. То есть ни что иное, как величина фиксированных затрат FC.

10 × Q + 2 × Q² + FC = 400

При Q = 10

10 × 10 + 2 × 10² + FC = 400

FC = 100