Задача №17. Расчёт валового выпуска, промежуточного потребления и ВВП на основе уравнения математической модели МОБ
Экономика (условно) состоит из двух секторов.
Информация о коэффициентах прямых затрат (размерность матрицы 2x2) и величине валового выпуска по каждому сектору приводится в таблице 1.
| Коэффициенты прямых затрат, aij | Валовой выпуск, Xi | |
|---|---|---|
| а11=0,6 | а12=0,5 | X1 =1892 |
| а21=0,3 | а22=0,2 | X2 =(x11+x21) / 1,5 |
Определите:
1) ВВП (Y1 + Y2), соотношение валового выпуска и ВВП, а также ВВП и промежуточного потребления;
2) экономическую эффективность производства (по показателю затратоемкости ВВП, равному отношению промежуточного потребления к ВВП, умноженному на 100%), если прямые затраты первой продукции на производство единицы второй продукции уменьшатся на 20%.
Примечание: Для расчетов постройте два уравнения по первой и второй строкам балансовой таблицы, используя уравнение ма-тематической модели межотраслевого баланса (обратите внимание на то, что в качестве известных величин в данном случае используется не показатель конечного спроса, а валовой выпуск).
Решение:
Уравнение математической модели межотраслевого баланса в общем виде имеет вид:
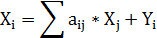
где
Xi – выпуск (ВВ) i-ой отрасли,
Хj – выпуск (ВВ) j-ой отрасли,
аij – коэффициенты прямых затрат продукции i-ой отрасли на производство единицы продукции j-ой отрасли (аij = xij : Хj),
Yi – конечный спрос i-ой отрасли (вклад i-ой отрасли в ВВП).
При решении обратим внимание на то, что в качестве неизвестных фигурируют компоненты ВВП (Y1 и Y2), а не суммарный продукт первой и второй отраслей экономики (Х1 и Х2), как в задачах №13, №14, №15.
Составим систему уравнений:
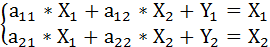 (1)
(1)
Показатель:
Х2 = (х11 + х21) / 1,5 = (а11 ∙ Х1 + а21 ∙ Х1) / 1,5 = (0,6 ∙ Х1 + 0,3 ∙ Х1) / 1,5 = 0,9 ∙ Х1 / 1,5 = 0,9 ∙ 1892 / 1,5 = 1135,2
Преобразуем систему уравнений (1) в новую систему из двух уравнений:
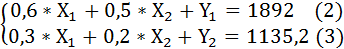
Из уравнения (2) определяем Y1:
Y1 = 1892 – 0,6 ∙ 1892 – 0,5 ∙ 1135,2 = 189,2
Из уравнения (3) определяем Y2:
Y2 = 1135,2 – 0,3 ∙ 1892 – 0,2 ∙ 1135,2 = 340,56
Тогда:
ВВП = 189,2 + 340,56 = 529,76
Валовой выпуск:
ВВ = 1892 + 1135,2 = 3027,2
Промежуточное потребление:
ПП= ВВ – ВВП = 3027,2 – 529,76 = 2497,44.
Валовой выпуск больше ВВП в 5,71 раза; ВВП составляет 21,21% от промежуточного потребления (529,76 * 100% / 2497,44).
2) Составим новую систему уравнений, если прямые затраты первой продукции на производство единицы второй продукции уменьшатся на 20%: с 0,5 до 0,8*0,5. То есть а12=0,4
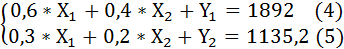
Из (4) уравнения определяем Y1:
Y1 = 1892 – 0,6 ∙ 1892 – 0,4 ∙ 1135,2 = 302,72.
Из (5) уравнения определяем Y2:
Y2 = 1135,2 – 0,3 ∙ 1892 – 0,2 ∙ 1135,2 = 340,56
Найдём ВВП:
ВВП = Y1 + Y2 = 302,72 + 340,56 = 643,28
Валовой выпуск остался прежним:
ВВ = 3027,2
Рассчитаем промежуточное потребление:
ПП = ВВ – ВВП = 3027,2 - 643,28 = 2383,92
Найдём показатель затратоёмкости ВВП до изменений. Он будет равен соотношению промежуточного потребления и ВВП:
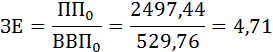
После уменьшения прямых затрат первой продукции на производство единицы второй продукции на 20% показатель затратоёмкости ВВП стал равен:
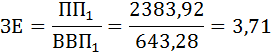
Показатель затратоёмкости снизился, следовательно, экономическая эффективность производства повысилась.

Экономическая прибыль

Счёт операций с капиталом
Смотри ещё
- Анализ рыночной структуры / Задача №135. Расчёт потерь монополиста в результате государственного вмешательства
- Анализ рыночной структуры / Задача №174. Расчёт параметров равновесия на рынке монополистической конкуренции
- Анализ рыночной структуры / Задача №197. Расчёт выпуска и цены лидера
- Анализ рыночной структуры / Задача №198. Лидерство в ценообразовании
- Деньги, банковская система и монетарная политика / Задача №34. Расчёт темпа инфляции в количественной теории денег
- Макроэкономическая нестабильность / Задача №51. Расчёт потенциального ВВП
- Макроэкономическая нестабильность / Задача №52. Расчёт фактического ВВП
- Макроэкономическая нестабильность / Задача №53. Расчёт коэффициента Оукена и естественного уровня безработицы
- Макроэкономическая нестабильность / Задача №54. Расчёт потенциального ВВП, фактического и естественного уровня безработицы
- Макроэкономическая нестабильность / Задача №55. Расчёт фактического ВВП и фактического уровеня безработицы
- Макроэкономическая нестабильность / Задача №57. Расчёт темпа изменения ВВП и определение фазы цикла
- Макроэкономическая нестабильность / Задача №58. Расчёт реального ВВП и определение причины спада
- Макроэкономическая нестабильность / Задача №59. Расчёт темпа инфляции и определение фазы цикла
- Макроэкономическая нестабильность / Задача №61. Расчёт потерь от безработицы
- Макроэкономическое равновесие / Задача №37. Определение величины ВВП и вида разрыва
- Макроэкономическое равновесие / Задача №68. Расчёт равновесного объема ВВП
- Макроэкономическое равновесие / Задача №79. Расчёт темпа инфляции в долгосрочном периоде
- Макроэкономическое равновесие / Задача №80. Расчёт относительного изменения равновесного уровня цен
- Основные макроэкономические показатели / Задача №1. Расчёт номинального и реального ВВП, дефлятора и ИПЦ
- Основные макроэкономические показатели / Задача №2. Расчёт номинального и реального ВВП, индексов Пааше, Ласпейреса и Фишера
- Основные макроэкономические показатели / Задача №16. Расчёт ВВП (двумя способами), ВНП, ЧНП, НД, ЛД, РЛД и др
- Основные макроэкономические показатели / Задача №17. Расчёт стоимости конечной и промежуточной продукции, ВВП и добавленной стоимости
- Основные макроэкономические показатели / Задача №19. Расчёт ВВП, ВНП, ЧВП, ЧНП, НД, ЛД, РЛД и др.
- Основные макроэкономические показатели / Задача №20. Расчёт реального ВВП, темпа прироста ВВП и темпа инфляции
- Основные макроэкономические показатели / Задача №21. Расчёт индекса-дефлятора ВВП
- Основные макроэкономические показатели / Задача №25. Расчёт чистого экспорта
- Основные макроэкономические показатели / Задача №26. Расчёт ВВП по доходам
- Основные макроэкономические показатели / Задача №27. Расчёт темпов прироста номинального ВВП, реального ВВП и дефлятора ВВП
- Основные макроэкономические показатели / Задача №62. Расчёт инвестиций
- Основные макроэкономические показатели / Задача №63. Расчёт частных сбережений

Счёт использования располагаемого дохода




















