Задача №2 Оценить структурную модель на идентификацию
Модифицированная модель Кейнса:
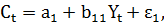
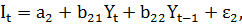
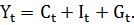
где
С – расходы на потребление;
Y – доход;
I – инвестиции;
G – государственные расходы;
t – текущий период;
t–1 – предыдущий период.
Применив необходимое и достаточное условие идентификации, определите, идентифицировано ли каждое из уравнений модели.
Определите метод оценки параметров модели.
Запишите приведённую форму модели.
Решение:
В этой модели три эндогенные переменные (Ct, It, Yt). Причём переменная Yt задана тождеством. Поэтому практически статистическое решение необходимо только для первых двух уравнений системы, которые необходимо проверить на идентификацию. Модель содержит две предопределённые переменные – экзогенную Gt и лаговую – Yt-1.
При практическом решении задачи на основе статистической информации за ряд лет или по совокупности регионов за один год в уравнениях для эндогенных переменных Ct, It обычно содержится свободный член (а1, а2), значение которого аккумулирует влияние неучтённых в уравнении факторов и не влияет на определение идентифицируемости модели.
Поскольку фактические данные об эндогенных переменных Ct, It могут отличаться от постулируемых моделью, то принято в модель включать случайную составляющую для каждого уравнения системы, исключив тождества. Случайные составляющие обозначены через ɛ1 и ε2. Они не влияют на решение вопроса об идентификации модели.
В рассматриваемой эконометрической модели в первом уравнении системы две эндогенных переменных Ct, It, т. е. H = 2, число отсутствующих предопределённых переменных также равно двум (Gt и Yt-1) – D = 2.
По счётному правилу D + 1 > H, то есть 2 + 1 > 2.
Следовательно, уравнение сверхидентифицируемо.
Коэффициенты при отсутствующих в первом уравнении переменных составят:
| Уравнения | Переменные | ||
| It | Yt-1 | Gt | |
| 2 | -1 | b22 | 0 |
| 3 | 1 | 0 | 1 |
Согласно таблице detA≠0, ранг матрицы равен двум, что соответствует следующему критерию: ранг матрицы коэффициентов должен быть не менее чем число эндогенных переменных в системе без одного. Достаточное условие идентификации выполняется.
Во втором уравнении системы две эндогенных переменных Yt, It, т. е. H = 2, число отсутствующих предопределённых переменных равно одному (Gt) – D = 1.
По счётному правилу D + 1 = H, то есть 1 + 1 = 2.
Следовательно, уравнение идентифицируемо.
Коэффициенты при отсутствующих во втором уравнении переменных составят:
| Уравнения | Переменные | |
| Ct | Gt | |
| 1 | -1 | 0 |
| 3 | 1 | 1 |
Согласно таблице detA≠0, ранг матрицы равен двум. Достаточное условие идентификации выполняется.
Тождество не требует проверки на идентификацию.
Так как модель содержит хотя бы одно сверхидентифицируемое уравнение, следовательно, в целом она сверхидентифицируема.
Для определения параметров сверхидентифицированной модели используется двухшаговый метод наименьших квадратов.
Запишем приведённую форму модели в общем виде:
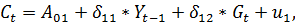
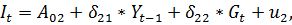
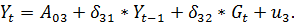
Где
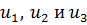 – случайные ошибки.
– случайные ошибки.
Условие задачи взято из: Практикум по эконометрике: Учеб. пособие/И.И. Елисеева, С.В. Курышева, Н.М. Гордиенко и др.; Под ред. И.И. Елисеевой. - М.: Финансы и статистика, 2003. - 192 с.: ил.

Экономическая прибыль

Счёт операций с капиталом

Счёт использования располагаемого дохода




















