Задача №106. Определение количества фирм в отрасли

Известно, что рынок бензина в стране X находится в условиях совершенной конкуренции. Спрос на бензин описывается уравнением:

Q_d = 200 - 20P

Средние издержки типичной бензоколонки равны:

АС = 5 + (Q - 5)²

Какое число бензоколонок должно действовать в отрасли в долгосрочной перспективе?

Решение:

Запишем функцию средних издержек в более удобном виде:

АС = 5 + (Q - 5)² = Q² - 10Q + 30

В долгосрочном периоде в положении равновесия цена равна предельным издержкам и равна минимуму средних общих издержек:

P = MC = min ATC.

Найдём минимум средних общих издержек. Приравняем к нулю производную средних общих издержек:

АТС' = (Q² - 10Q + 30)' = 2Q - 10

2Q - 10 = 0

Q = 5 - это уровень производства одной фирмы при минимуме средних затрат.

Рассчитаем минимум средних затрат при Q = 5:

АС (5) = 52 - 10*5 + 30 = 5

Так как цена предложения каждой фирмы в условиях равновесия равна минимуму средних затрат, то есть равна 5, можно подставить это значение цены в функцию спроса и найти равновесный объём в отрасли. Рыночный спрос будет равен:

Q_d = 200 - 20*5 = 100

Значит и рыночное предложение равно 100 единицам.

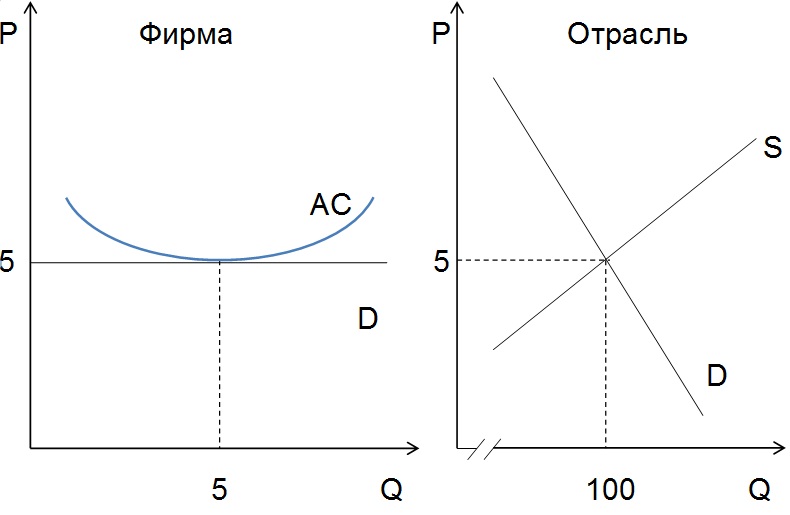
Соответственно, если каждое предприятие производит 5 единиц продукции, а все предприятия в отрасли - 100 единиц, их количество определяется делением рыночного предложения на выпуск одного из них:

n = Q_отр / Q = 100 / 5 = 20