Задача №113. Определение оптимального выпуска фирмы

В отрасли совершенной конкуренции установилась цена:

Р = 50

Средние переменные затраты конкурентной фирмы выражены формулой:

AVC = 50 + (Q – 30)²

Фиксированные затраты равны 10 000.

Найти оптимальный выпуск фирмы.

Решение:

Оптимум фирмы, действующей на рынке совершенной конкуренции, достигается при условии равенства предельных затрат и цены:

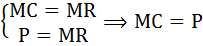
Найдём предельные затраты. Для этого необходимо знать функцию общих затрат или функцию переменных затрат. Общие издержки в краткосрочном периоде состоят из постоянных и переменных. По условию нам известна величина постоянных затрат, а также дана функция средних переменных затрат. Можно найти функцию переменных затрат по формуле:

VC = AVC × Q = (50 + (Q – 30)²) × Q = (50 + Q² – 60 × Q + 900) × Q = Q³ – 60 × Q² + + 950 × Q

Тогда функция общих затрат будет иметь вид:

ТС = Q³ – 60 × Q² + 950 × Q + 10 000.

Найдём функцию предельных затрат.

МС = (ТС)’ = (Q³ – 60 × Q² + 950 × Q + 10 000)’ = 3 × Q² – 120 × Q + 950

Нетрудно заметить, что тот же результат получился бы при дифференцировании функции переменных затрат.

Вернёмся к условию оптимума фирмы:

МС = Р

3 × Q² – 120 × Q + 950 = 50

3 × Q² – 120 × Q + 900 = 0

Решая данное квадратное уравнение, получаем два корня:

Q₁ = 30 и Q₂ = 10.

Встаёт вопрос, какой из них выбрать.

Из двух полученных значений необходимо выбрать то, которое соответствует возрастающему участку кривой МС.

Найдём минимум МС. Для нахождения экстремума функции приравняем к нулю её производную.

6Q – 120 = 0

Q = 20.

Значит, восходящему участку кривой соответствует значение выпуска:

Q = 30 – это и есть оптимальный выпуск фирмы.