Задача №122. Расчёт эластичности спроса по цене
Функция спроса на продукцию монополиста:
P = 20 - 2 × Q,
MC = AC = 4.
Найти эластичность спроса по цене, если монополист ищет максимум прибыли.
Решение:
Эластичность спроса по цене рассчитывается по формуле:
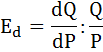 ,
,
где
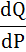 - производная функции спроса Q(P) по аргументу Р.
- производная функции спроса Q(P) по аргументу Р.
По условию задачи функция спроса на продукцию монополиста:
P = 20 - 2 × Q.
Это обратная функция спроса. Выразив отсюда Q, получим прямую функцию спроса:
Q = 10 - 0,5 × P,
производная которой и потребуется нам при нахождении эластичности спроса по цене.
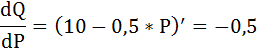
Осталось найти координаты точки оптимума. То есть такой оптимальный объём производства и цену, при которых монополист максимизирует свою прибыль.
Условие максимизации прибыли на рынке несовершенной конкуренции имеет вид:
MC = MR
Предельные издержки по условию равны
MC = 4.
Найдём величину общего дохода по формуле:
TR = Р × Q = (20 - 2 × Q) × Q = 20 × Q - 2 × Q2
Тогда предельный доход будет равен:
MR = TR' = (20 × Q - 2 × Q2)' = 20 - 4 × Q
4 = 20 - 4 × Q
Q = 4 - это оптимальный объём выпуска монополиста.
Цену найдём из функции спроса:
P = 20 - 2 × 4 = 12.
Рассчитаем эластичность спроса по цене:
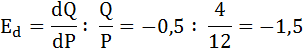

Экономическая прибыль

Счёт операций с капиталом

Счёт использования располагаемого дохода
Смотри ещё
- Производство и затраты фирмы / Задача №196. Расчёт оптимума производства
- Рынки факторов производства / Задача №165. Расчёт количества закупаемого фактора
- Рынки факторов производства / Задача №167. Расчёт цены на продукцию фирмы
- Спрос и предложение / Задача №1. Определение изменения дохода при увеличении проданной продукции на одну единицу
- Спрос и предложение / Задача №2. Коэффициент точечной эластичности
- Спрос и предложение / Задача №3. Эластичность спроса по цене
- Спрос и предложение / Задача №4. Функция суммарного спроса
- Спрос и предложение / Задача №5. Функция суммарного спроса
- Спрос и предложение / Задача №6. Расчёт дуговой эластичности
- Спрос и предложение / Задача №7. Расчёт дуговой эластичности
- Спрос и предложение / Задача №8. Расчёт точечной эластичности
- Спрос и предложение / Задача №9. Расчёт точечной эластичности
- Спрос и предложение / Задача №10. Расчёт первоначального объёма рыночного спроса
- Спрос и предложение / Задача №11. Расчёт выручки
- Спрос и предложение / Задача №14. Точечная и дуговая эластичность спроса по цене
- Спрос и предложение / Задача №15. Дуговая эластичность спроса
- Спрос и предложение / Задача №16. Формула эластичности спроса
- Спрос и предложение / Задача №17. Точечная эластичность спроса по цене
- Спрос и предложение / Задача №18. Определение характера взаимосвязи товаров
- Спрос и предложение / Задача №19. Определение категории товара
- Спрос и предложение / Задача №20. Прямая и перекрёстная эластичность спроса по цене
- Спрос и предложение / Задача №21. Коэффициенты прямой и перекрёстной эластичности спроса
- Спрос и предложение / Задача №23. Расчёт изменения доли расходов
- Спрос и предложение / Задача №24. Эластичность спроса по доходу
- Спрос и предложение / Задача №25. Вычисление перекрёстной эластичности спроса
- Спрос и предложение / Задача №26. Расчёт ценовой эластичности спроса
- Спрос и предложение / Задача №28. Расчёт эластичности спроса
- Спрос и предложение / Задача №30. Сколько пакетов сока будет продано
- Спрос и предложение / Задача №31. Коэффициент прямой эластичности спроса
- Спрос и предложение / Задача №32. Коэффициент эластичности предложения




















