Задача №114. Определение прямой и обратной функции предложения

Функция общих затрат совершенно конкурентной фирмы имеет вид:

ТС = Q³ - 16Q² + 100Q + 500.

Запишите уравнение прямой и обратной функции предложения данной фирмы в краткосрочном периоде.

Решение:

1. Фирма максимизирует выпуск в краткосрочном периоде, если цена продукта равна предельным издержкам:

Р = МС

Определим величину предельных издержек. Возьмём первую производную от функции общих издержек:

МС = (ТС)' = (Q³ - 16Q² + 100Q + 500)' = 3Q² - 32Q + 100

P = 3Q² - 32Q + 100 - это и есть обратная функция предложения фирмы совершенного конкурента.

Найдём область допустимых значений этой функции.

Функция предложения фирмы совпадает c восходящим участком функции предельных издержек, начиная с точки минимума средних переменных издержек, включая эту точку.

Найдём эту точку минимума. Выделим из функции общих издержек величину переменных издержек:

VC = Q³ - 16Q² + 100Q

Средние переменные издержки определим по формуле:

AVC = VC / Q = (Q³ - 16Q² + 100Q) / Q = Q² - 16Q + 100.

Определим минимум этой функции. Приравняем к нулю её производную и найдём Q, при котором средние переменные издержки будут минимальны.

AVC' = 0

(Q² - 16Q + 100)' = 0

2Q - 16 = 0

Q = 8

При Q = 8 минимум средних переменных издержек будет равен:

AVC_min = 8² - 16 × 8 + 100 = 36

Таким образом, обратная функция предложения имеет вид:

P_s = 3 × Q² - 32 × Q + 100 при Q ≥ 8.

2. Запишем уравнение прямой функции предложения.

Функция предложения фирмы в краткосрочном периоде на рынке совершенной конкуренции имеет вид:

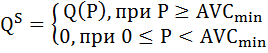
Решим квадратное уравнение:

P = 3 × Q² - 32 × Q + 100

3 × Q² - 32 × Q + 100 - Р = 0

D = b² - 4ac = 32² - 4 × 3 × (100 - P) = 1024 - 12 × (100 - P) = 12P - 176

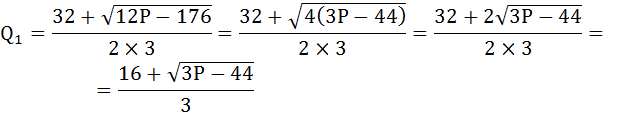
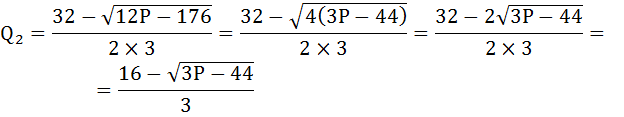
Выберем решение Q₁ с положительным знаком, так как при Q₂ максимизируются убытки, а не прибыль.

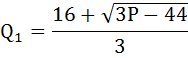
Уравнение прямой функции предложения фирмы в краткосрочном периоде имеет вид.

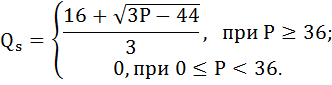
Условие задачи заимствовано из: Акимов Д.В. Задания по экономике: от простых до олимпиадных. Пособие для 10-11 классов общеобразоват. учрежд. /Д. В. Акимов, О. В. Дичева, Л. Б. Щукина. - М. : Вита-Пресс, 2008. - 320 с.: ил.