Задача №104. Расчёт рыночной цены и объёма выпуска на конкурентном рынке

Конкурентная фирма имеет предельные затраты:

МС = 30 + 2 × Q

при фиксированных затратах, равных 500 денежным единицам.

Она получает в краткосрочном периоде максимально возможную прибыль, равную 1100 денежным единицам.

Определить цену на рынке и объём выпуска данной фирмы.

Решение:

Формула прибыли имеет вид:

П = TR – TC = P*Q – TC

Определим функцию общих затрат. Так как функция предельных затрат это производная функции общих затрат, следовательно, функцию общих затрат можно определить как первообразную от функции предельных затрат.

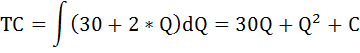
где

С – константа, равная величине фиксированных затрат, которые по условию равны 500.

Таким образом функция общих затрат имеет вид:

ТС = Q² +30*Q + 500

Теперь запишем условие максимизации прибыли на рынке совершенной конкуренции в краткосрочном периоде:
Р = МС = MR = AR

Воспользуемся тем, что:

Р = МС

По условию задачи:

МС = 30 + 2 × Q, то есть Р = 30 + 2 * Q

Подставим это выражение, а так же функцию общих затрат в формулу прибыли и получим уравнение с одной неизвестной.

(30 + 2 * Q) * Q – (Q² +30*Q + 500) = 1100
Q2 = 1600
Q = ± 40

Так как отрицательное значение Q экономического смысла не имеет, следовательно, объём выпуска данной фирмы Q = 40.

Тогда рыночная цена будет равна:

Р = 30 + 2 * 40 = 110.