Задача №169. Нахождение уравнений кривых спроса и предложения

Спрос и предложение на рынке на товар задаются линейными уравнениями. Известно, что равновесная цена равна 200 руб. за упаковку товара, а равновесное количество - 100 упаковок в день. В точке равновесия однопроцентное повышение цены на данный товар влечет снижение величины спроса на 1,5% и повышение величины предложения на 0,5%.

Определите уравнения кривых спроса и предложения, считая их линейными.
 

Решение:

Общая точка двух прямых спроса и предложения имеет координаты:

Q = 100, Р = 200.

Общий вид линейной функции спроса:

Q_d = a – b × P

Так как однопроцентное повышение цены на данный товар влечет снижение величины спроса на 1,5%, следовательно, коэффициент эластичности спроса равен:

E_d = – 1,5

Запишем формулу точечной эластичности спроса по цене:

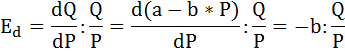
Подставим имеющиеся по условию данные:

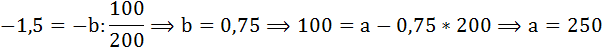
Тогда функция спроса на данный товар имеет вид:

Q_d = 250 – 0,75 × P

Общий вид линейной функции предложения:

Q_s = c + d × P

Так как однопроцентное повышение цены на данный товар влечет повышение величины предложения на 0,5%., следовательно, коэффициент эластичности предложения равен:

E_s = 0,5

Формула эластичности предложения будет иметь вид:

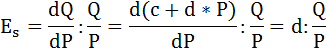
Подставим имеющиеся по условию данные:

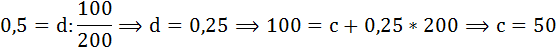
Тогда функция предложения на данный товар имеет вид:

Q_s = 50 + 0,25 × P