Задача №164. Расчёт оптимального выпуска продукции

Фирма находится в условиях совершенной конкуренции на рынке данного товара и труда. Ее производственная функция имеет вид

Q = 120 × L – 2 × L ²

в интервале использования труда от 12 до 30 единиц. Ставка заработной платы равна 60 ден. ед., а цена товара 8 ден. ед. Определить оптимальный для фирмы выпуск продукции.

Решение:

Общее условие максимизации прибыли при покупке фактора производства.

Для того чтобы получить максимальную прибыль произведя и продав продукцию на рынке готовой продукции фирма на рынке труда должна нанять такое количество работников, чтобы выполнялось следующее:

MRP_L = MIC

где

MRP_L – предельная доходность труда,

МIC – предельные издержки на фактор производства (труд).

MRP_L = MR × MP_L

где

MR – предельная выручка,

MP_L – предельный продукт труда.

Фирма находится в условиях совершенной конкуренции на рынке данного товара и на рынке труда.

Фирма, продающая продукцию на совершенно конкурентном рынке, не может повлиять на рыночную цену, она принимает её как заданную и в этом случае:

Р = МR

На рынке труда издержки фирмы на труд равны ставке заработной платы:

MIC = ω,

где

ω – ставка заработной платы

Таким образом, для совершенно конкурентной во всех отношениях фирмы условие максимизации прибыли при покупке фактора производства будет иметь вид:

P × MP_L = ω

Продифференцируем производственную функцию и найдём предельный продукт труда (MP_L) по формуле:

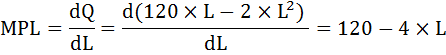
Подставим это выражение в условие максимизации прибыли и найдём количество нанимаемого труда:

8 × (120 – 4 × L) = 60

960 – 32 × L = 60

900 = 32 × L

L = 28,125

Оптимальный для фирмы выпуск продукции будет равен:

Q = 120 × 28,125 – 2 × 28,125 ² = 1793