Задача №32. Расчёт предела, в котором находится средний возраст рабочих
На заводе, где число рабочих составляет 1000 человек, было проведено выборочное обследование возраста рабочих. Методом случайного бесповторного отбора было отобрано 50 человек. Результаты обследования следующие:
| Возраст рабочих (лет) | до 30 | 30 – 40 | 40 – 50 | 50 – 60 | свыше 60 |
|---|---|---|---|---|---|
| Число рабочих | 8 | 22 | 10 | 6 | 4 |
С вероятностью 0,997 определите предел, в котором находится средний возраст рабочих завода.
Решение:
1. Рассчитаем средний возраст рабочих завода в выборочной совокупности. Все расчёты оформим в таблицу.
| Возраст рабочих (лет) | Число рабочих (f) | Среднее значение интервала (х) | 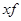 |
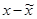 |
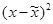 |
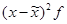 |
|---|---|---|---|---|---|---|
| до 30 | 8 | 25 | 200 | -15,2 | 231,04 | 1848,3 |
| 30 – 40 | 22 | 35 | 770 | -5,2 | 27,04 | 594,88 |
| 40 – 50 | 10 | 45 | 450 | 4,8 | 23,04 | 230,4 |
| 50 – 60 | 6 | 55 | 330 | 14,8 | 219,04 | 1314,2 |
| свыше 60 | 4 | 65 | 260 | 24,8 | 615,04 | 2460,2 |
| Итого: | 50 | - | 2010 | - | - | 6448 |
Средняя выборочная в данном случае будет рассчитываться по формуле средней арифметической взвешенной:
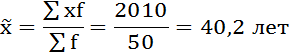
2. Рассчитаем дисперсию выборочной совокупности:
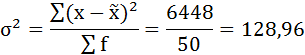
3. Средняя ошибка выборки составит:
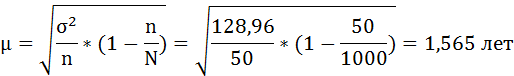
4. С вероятностью 0,997 рассчитаем предельную ошибку выборочной средней.
Δ = μ * t
t - коэффициент доверия.
Значение коэффициента доверия t определяется в зависимости от того, с какой доверительной вероятностью надо гарантировать результаты выборочного наблюдения и берётся из готовых таблиц.
Наиболее часто встречающиеся в задачах подобного рода значения t:
| Вероятность Р | 0,683 | 0,866 | 0,954 | 0,988 | 0,997 | 0,999 |
|---|---|---|---|---|---|---|
| Значение t | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 |
При Р = 0,997, t = 3.
Δ = 1,565 * 3 = 4,696 лет.
5. Определим пределы, в которых находится средний возраст рабочих завода.
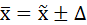
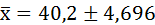
Генеральная средняя (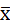 ) находится в пределах
) находится в пределах
40,2 - 4,696 ˂ 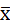 ˂ 40,2 + 4,696.
˂ 40,2 + 4,696.
35,5 ˂ 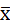 ˂ 44,9
˂ 44,9
С вероятностью 0,997 можно утверждать, что средний возраст рабочих завода находится в пределах 35,5 ˂ 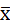 ˂ 44,9 лет.
˂ 44,9 лет.

Рыночное равновесие
Смотри ещё
- Выборочное наблюдение / Задача №33. Расчёт предела, в котором находится средняя крепость пряжи в партии
- Выборочное наблюдение / Задача №36. Расчёт необходимой численности выборки при механическом отборе
- Выборочное наблюдение / Задача №37. Расчёт необходимой численности выборки
- Выборочное наблюдение / Задача №38. Расчет необходимой численности выборки для определения доли
- Выборочное наблюдение / Задача №39. Расчёт предела, в котором находятся средние затраты времени
- Выборочное наблюдение / Задача №51. Расчёт ошибки выборочной доли
- Основные макроэкономические показатели / Задача №21. Расчёт индекса-дефлятора ВВП
- Средние величины и показатели вариации / Задача №1. Расчёт средней арифметической, модального и медианного значения
- Средние величины и показатели вариации / Задача №4. Расчёт средней заработной платы
- Средние величины и показатели вариации / Задача №5. Расчёт средней арифметической взвешенной в интервальном ряду распределения
- Средние величины и показатели вариации / Задача №6. Расчёт показателей вариации
- Средние величины и показатели вариации / Задача №7. Расчёт коэффициента вариации
- Средние величины и показатели вариации / Задача №8. Расчёт средней
- Средние величины и показатели вариации / Задача №9. Расчёт среднего квадрата индивидуальных значений признака
- Средние величины и показатели вариации / Задача №10. Расчёт среднего квадрата отклонений вариантов признака от произвольной величины
- Средние величины и показатели вариации / Задача №11. Расчёт дисперсии признака
- Средние величины и показатели вариации / Задача №12. Расчёт коэффициента вариации
- Средние величины и показатели вариации / Задача №13. Расчёт среднего квадрата отклонений индивидуальных значений признака от произвольной величины
- Средние величины и показатели вариации / Задача №22. Виды дисперсии и их расчёт
- Средние величины и показатели вариации / Задача №23. Расчёт показателей асимметрии и эксцесса
- Средние величины и показатели вариации / Задача №24. Расчёт показателей вариации по несгруппированным данным
- Средние величины и показатели вариации / Задача №27. Расчёт средней себестоимости
- Средние величины и показатели вариации / Задача №28. Расчёт среднего процента выполнения плана выпуска продукции
- Средние величины и показатели вариации / Задача №43. Расчёт описательных статистик
- Средние величины и показатели вариации / Задача №45. Расчёт абсолютных и относительных показателей вариации
- Статистика населения / Задача №2. Расчёт средней численности населения
- Статистика населения / Задача №3. Расчёт средней численности населения
- Статистические методы изучения взаимосвязей / Задача №47. Построение модели линейной регрессии
- Эконометрика / Задача №1 Построение уравнения регрессии
- Эконометрика / Задача №4. Построение регрессионной модели с использованием фиктивной переменной






















