Задача №23. Расчёт показателей асимметрии и эксцесса
Распределение коммерческих банков по размеру активов характеризуется следующими данными:
| Размер активов, млн руб. | До 200 | 200 - 300 | 300 - 400 | 400 - 500 | 500 - 600 | 600 и более | Итого |
|---|---|---|---|---|---|---|---|
| Удельный вес банков, % к итогу | 8 | 25 | 52 | 7 | 5 | 3 | 100 |
Определите характеристики распределения:
а) среднюю;
б) моду;
в) среднее квадратическое отклонение;
г) коэффициент вариации;
д) коэффициент асимметрии и эксцесс.
Решение:
Данный интервальный вариационный ряд содержит открытые интервалы, которые предварительно необходимо закрыть. Для этого из величины верхней границы первого интервала надо вычесть величину второго интервала. Получим нижнюю границу первого интервала.
200 - 100 = 100.
Первый интервал: 100 - 200.
Теперь к нижней границе последнего интервала прибавляем величину предшествующего интервала:
600 + 100 = 700
Последний интервал: 600 - 700.
а) Определение средней по сгруппированным данным производится по формуле средней арифметической взвешенной:
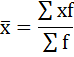
Чтобы применить эту формулу, необходимо варианты признака выразить одним числом (дискретным). За такое дискретное число принимается средняя арифметическая простая из верхнего и нижнего значения каждого интервала.
Так, например, дискретная величина х для первого интервала будет равна: (100 + 200) / 2 = 150.
Построим таблицу рассчётных данных:
| х | f | хf | 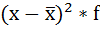 | 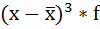 | 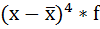 |
|---|---|---|---|---|---|
| 150 | 8 | 1 200 | 273800 | -50 653 000 | 9 370 805 000 |
| 250 | 25 | 6 250 | 180625 | -15 353 125 | 1 305 015 625 |
| 350 | 52 | 18 200 | 11700 | 175 500 | 2 632 500 |
| 450 | 7 | 3 150 | 92575 | 10 646 125 | 1 224 304 375 |
| 550 | 5 | 2 750 | 231125 | 49 691 875 | 10 683 753 125 |
| 650 | 3 | 1 950 | 297675 | 93 767 625 | 29 536 801 875 |
| Итого | 100 | 33 500 | 1087500 | 88 275 000 | 52 123 312 500 |
Дальнейший расчёт производится обычным методом определения средней арифметической взвешенной.
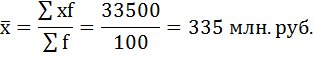
б) Определим моду.
Мода - это величина признака наиболее часто встречающегося в совокупности.
В интервальных рядах распределения с равными интервалами мода определяется по формуле:
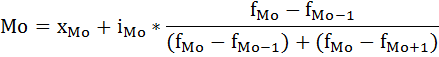
где
хМо – начальное значение интервала, содержащего моду;
iМо – величина модального интервала,
fМо – частота модального интервала,
fМо-1 – частота интервала, предшествующего модальному,
fМо+1 – частота интервала, следующего за модальным.
Мода содержится в интервале от 300 до 400, так как у этого интервала наибоьшая частота
f = 52.
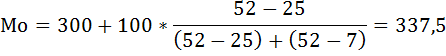 млн. руб.
млн. руб.
в) Найдём среднее квадратическое отклонение:
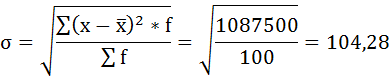
Значения размера активов в ряду распределения могут отличаться от среднего значения на 104,28 млн. руб.
Дисперсия будет равна:
σ2 = 10 875
г) Коэффициент вариации рассчитаем по формуле:
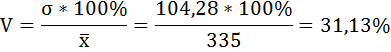
Совокупность однородна, так как коэффициент вариации не превышает 33%.
д) Рассчитаем показатель асимметрии через отношение центрального момента третьего порядка к среднему квадратическому отклонению данного ряда в кубе, то есть
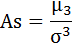
где μ3 - центральный момент третьего порядка, рассчитываемый по формуле:
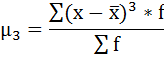
μ3 = 88 275 000 / 100 = 882 750
As = 882 750 / 104,283 = 0,78
Так как величина показателя асимметрии положительна, следовательно, речь идёт о правосторонней асимметрии.
Полученный результат свидетельствует о наличии несущественной по величине и положительной по своему характеру асимметрии.
Далее рассчитаем показатель эксцесса (Еk). Наиболее точно он определяется по формуле с использованием центрального момента четвёртого порядка:
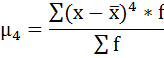
μ4 = 52 123 312 500 / 100 = 521 233 125
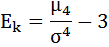
σ4 = 118 265 625
Ek = 521 233 125 / 118 265 625 – 3 = 4,41 - 3 = 1,41
Так как Ek > 0 распределение является островершинным.
Смотри ещё
- Выборочное наблюдение / Задача №32. Расчёт предела, в котором находится средний возраст рабочих
- Выборочное наблюдение / Задача №39. Расчёт предела, в котором находятся средние затраты времени
- Основные макроэкономические показатели / Задача №21. Расчёт индекса-дефлятора ВВП
- Средние величины и показатели вариации / Задача №1. Расчёт средней арифметической, модального и медианного значения
- Средние величины и показатели вариации / Задача №4. Расчёт средней заработной платы
- Средние величины и показатели вариации / Задача №5. Расчёт средней арифметической взвешенной в интервальном ряду распределения
- Средние величины и показатели вариации / Задача №6. Расчёт показателей вариации
- Средние величины и показатели вариации / Задача №7. Расчёт коэффициента вариации
- Средние величины и показатели вариации / Задача №9. Расчёт среднего квадрата индивидуальных значений признака
- Средние величины и показатели вариации / Задача №12. Расчёт коэффициента вариации
- Средние величины и показатели вариации / Задача №13. Расчёт среднего квадрата отклонений индивидуальных значений признака от произвольной величины
- Средние величины и показатели вариации / Задача №24. Расчёт показателей вариации по несгруппированным данным
- Средние величины и показатели вариации / Задача №27. Расчёт средней себестоимости
- Средние величины и показатели вариации / Задача №28. Расчёт среднего процента выполнения плана выпуска продукции
- Средние величины и показатели вариации / Задача №29. Расчёт крайних значений вариационного ряда
- Средние величины и показатели вариации / Задача №30. Расчёт коэффициента вариации
- Средние величины и показатели вариации / Задача №43. Расчёт описательных статистик
- Средние величины и показатели вариации / Задача №45. Расчёт абсолютных и относительных показателей вариации
- Средние величины и показатели вариации / Задача №46. Определение моды и медианы в дискретном ряду
- Средние величины и показатели вариации / Задача №48. Расчёт показателей вариации
- Статистика населения / Задача №2. Расчёт средней численности населения
- Статистика населения / Задача №3. Расчёт средней численности населения
- Статистические методы изучения взаимосвязей / Задача №47. Построение модели линейной регрессии
- Эконометрика / Задача №1 Построение уравнения регрессии
- Эконометрика / Задача №4. Построение регрессионной модели с использованием фиктивной переменной























