Задача №1. Расчёт средней арифметической, модального и медианного значения
Распределение торговых фирм по размеру месячного товарооборота характеризуется следующими данными:
| №п/п | Товарооборот, млн. руб. | Число фирм |
| 1 | до 5 | 20 |
| 2 | 5-10 | 26 |
| 3 | 10-15 | 20 |
| 4 | 15-20 | 14 |
| 5 | 20-25 | 10 |
| 6 | 25 и более | 10 |
| Итого | - | 100 |
Определите:
а) средний размер месячного товарооборота на одну фирму;
б) модальное и медианное значение месячного товарооборота;
в) сделайте выводы о характере данного распределения.
Решение:
а) Рассчитаем средний размер товарооборота на одну фирму.
В данном ряду варианты усредняемого признака (товарооборот) представлены не одним числом, а в виде интервала «от – до». Причём первый и последний – интервалы открытые.
В таких рядах условно принимается, величина интервала первой группы равна величине интервала последующей, а величина интервала последней группы равна величине интервала предыдущей. Таким образом, товарооборот первой группы от 0 до 5 млн. руб., товарооборот последней – от 25 до 30 млн. руб. Исчисление средней по сгруппированным данным производится по формуле средней арифметической взвешенной:
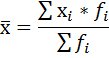
Чтобы применить эту формулу, необходимо варианты признака выразить одним числом (дискретным). За такое дискретное число принимается средняя арифметическая простая из верхнего и нижнего значения интервала. Так для первой группы дискретная величина х будет равна: (0 + 5) / 2 = 2,5. Дальнейший расчёт производится обычным методом определения средней арифметической взвешенной:
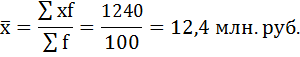
Исходные и расчётные данные представим в таблице:
| Товарооборот, млн. руб. | Число фирм, f | Середина интервала, х | xf | Сумма накопленных частот |
| 0-5 | 20 | 2,5 | 50 | 20 |
| 5-10 | 26 | 7,5 | 195 | 46 |
| 10-15 | 20 | 12,5 | 250 | 66 |
| 15-20 | 14 | 17,5 | 245 | - |
| 20-25 | 10 | 22,5 | 225 | - |
| 25-30 | 10 | 27,5 | 275 | - |
| Итого | 100 | - | 1240 | - |
б) Определим модальное и медианное значение месячного товарооборота.
В интервальных рядах распределения с равными интервалами мода определяется по формуле:
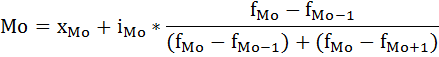
xMo – начальное значение интервала, содержащего моду;
iMo – величина модального интервала,
fMo – частота модального интервала,
f(Mo-1) – частота интервала, предшествующего модальному,
f(Mo+1) – частота интервала, следующего за модальным.
Наибольшее число фирм (26) имеют величину товарооборота от 5 до 10 млн. руб. Следовательно, этот интервал является модальным интервалом ряда распределения. Введём следующие обозначения:
xMo=5, iMo=5, fMo=26, f(Mo-1)=20, f(Mo+1)=20.
Подставим эти значения в формулу моды и произведём вычисления:
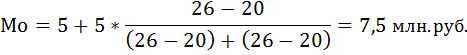
Следовательно, наибольшее число фирм имеет товарооборот 7,5 млн. руб.
Медиана интервального вариационного ряда распределения определяется по формуле:
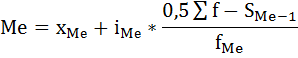
где xMе – начальное значение интервала, содержащего медиану;
iMе – величина медианного интервала;
Σf – сумма частот ряда;
S(Me-1) – сумма накопленных частот, предшествующих медианному интервалу;
fMe – частота медианного интервала.
Определим, прежде всего, медианный интервал. Сумма накопленных частот, превышающая половину всех значений (66), соответствует интервалу 10 – 15. Это и есть медианный интервал, в котором находится медиана. Определим её значение по приведённой выше формуле, если:
xMе=10, iMе=5, Σf=100, S(Me-1)=46, fMe=20:
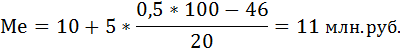
Таким образом, половина фирм имеет товарооборот менее 11 млн. руб., а остальные фирмы – более 11 млн. руб.
в) В симметричных рядах распределения значения моды и медианы совпадают со средней величиной, а в умеренно ассиметричных они соотносятся таким образом:
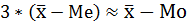
Соотношение характеристик центра распределения товарооборота свидетельствует об умеренной асимметрии:
3(12,4-11) ≈12,4-7,5
Смотри ещё
- Выборочное наблюдение / Задача №32. Расчёт предела, в котором находится средний возраст рабочих
- Основные макроэкономические показатели / Задача №21. Расчёт индекса-дефлятора ВВП
- Средние величины и показатели вариации / Задача №3. Расчёт среднего времени
- Средние величины и показатели вариации / Задача №4. Расчёт средней заработной платы
- Средние величины и показатели вариации / Задача №5. Расчёт средней арифметической взвешенной в интервальном ряду распределения
- Средние величины и показатели вариации / Задача №6. Расчёт показателей вариации
- Средние величины и показатели вариации / Задача №23. Расчёт показателей асимметрии и эксцесса
- Средние величины и показатели вариации / Задача №24. Расчёт показателей вариации по несгруппированным данным
- Средние величины и показатели вариации / Задача №26. Расчёт среднего удоя
- Средние величины и показатели вариации / Задача №27. Расчёт средней себестоимости
- Средние величины и показатели вариации / Задача №28. Расчёт среднего процента выполнения плана выпуска продукции
- Средние величины и показатели вариации / Задача №43. Расчёт описательных статистик
- Средние величины и показатели вариации / Задача №45. Расчёт абсолютных и относительных показателей вариации
- Средние величины и показатели вариации / Задача №46. Определение моды и медианы в дискретном ряду
- Средние величины и показатели вариации / Задача №48. Расчёт показателей вариации
- Статистика населения / Задача №2. Расчёт средней численности населения
- Статистика населения / Задача №3. Расчёт средней численности населения
- Статистика населения / Задача №11. Расчёт коэффициентов брачности и разводимости
- Статистические методы изучения взаимосвязей / Задача №47. Построение модели линейной регрессии























