Задача №5. Построение автокорреляционной функции
Имеются условные данные об объемах потребления электроэнергии yt жителями региона за 16 кварталов.
| t | yt | t | yt |
|---|---|---|---|
| 1 | 5,6 | 9 | 8,2 |
| 2 | 4,7 | 10 | 5,6 |
| 3 | 5,2 | 11 | 6,4 |
| 4 | 9,1 | 12 | 10,8 |
| 5 | 7,0 | 13 | 9,1 |
| 6 | 5,1 | 14 | 6,7 |
| 7 | 6,0 | 15 | 7,5 |
| 8 | 10,2 | 16 | 11,3 |
Требуется:
1. Построить автокорреляционную функцию и сделать вывод о наличии сезонных колебаний.
2. Построить аддитивную модель временного ряда.
3. Сделать прогноз на 2 квартала вперед.
Решение:
1. Рассчитаем коэффициент автокорреляции уровней ряда первого порядка, то есть между соседними уровнями ряда yt и yt-1 (лаг = 1), и измерим тесноту связи между объёмом потребления электроэнергии в текущем и предыдущем году.
Для этого составим таблицу расчётных данных.
Расчёт коэффициента автокорреляции первого порядка для временного ряда объемов потребления электроэнергии жителями региона:
| t | yt | yt-1 | 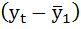 |
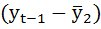 |
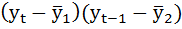 |
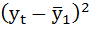 |
 |
|---|---|---|---|---|---|---|---|
| 1 | 5,6 | - | - | - | - | - | - |
| 2 | 4,7 | 5,6 | -2,827 | -1,547 | 4,371911 | 7,990044 | 2,392178 |
| 3 | 5,2 | 4,7 | -2,327 | -2,447 | 5,692578 | 5,413378 | 5,986178 |
| 4 | 9,1 | 5,2 | 1,573 | -1,947 | -3,06276 | 2,475378 | 3,789511 |
| 5 | 7 | 9,1 | -0,527 | 1,953 | -1,02876 | 0,277378 | 3,815511 |
| 6 | 5,1 | 7 | -2,427 | -0,147 | 0,355911 | 5,888711 | 0,021511 |
| 7 | 6 | 5,1 | -1,527 | -2,047 | 3,124578 | 2,330711 | 4,188844 |
| 8 | 10,2 | 6 | 2,673 | -1,147 | -3,06542 | 7,146711 | 1,314844 |
| 9 | 8,2 | 10,2 | 0,673 | 3,053 | 2,055911 | 0,453378 | 9,322844 |
| 10 | 5,6 | 8,2 | -1,927 | 1,053 | -2,02942 | 3,712044 | 1,109511 |
| 11 | 6,4 | 5,6 | -1,127 | -1,547 | 1,742578 | 1,269378 | 2,392178 |
| 12 | 10,8 | 6,4 | 3,273 | -0,747 | -2,44409 | 10,71471 | 0,557511 |
| 13 | 9,1 | 10,8 | 1,573 | 3,653 | 5,747911 | 2,475378 | 13,34684 |
| 14 | 6,7 | 9,1 | -0,827 | 1,953 | -1,61476 | 0,683378 | 3,815511 |
| 15 | 7,5 | 6,7 | -0,027 | -0,447 | 0,011911 | 0,000711 | 0,199511 |
| 16 | 11,3 | 7,5 | 3,773 | 0,353 | 1,333244 | 14,23804 | 0,124844 |
| Итого | 112,9 | 107,2 | - | - | 11,19133 | 65,06933 | 52,37733 |
Рассчитаем выборочные средние:
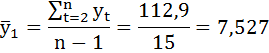
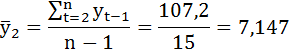
Определим коэффициент автокорреляции уровней ряда первого порядка:
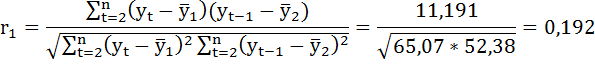
Полученное значение свидетельствует об очень слабой зависимости текущих уровней ряда от непосредственно им предшествующих уровней.
Рассчитаем коэффициент автокорреляции 2-го порядка.
| t | yt | yt-2 | 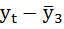 |
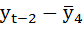 |
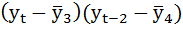 |
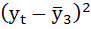 |
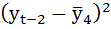 |
|---|---|---|---|---|---|---|---|
| 1 | 5,6 | - | - | - | - | - | - |
| 2 | 4,7 | - | - | - | - | - | - |
| 3 | 5,2 | 5,6 | -2,529 | -1,521 | 3,847041 | 6,393673 | 2,314745 |
| 4 | 9,1 | 4,7 | 1,371 | -2,421 | -3,32082 | 1,880816 | 5,863316 |
| 5 | 7 | 5,2 | -0,729 | -1,921 | 1,399898 | 0,530816 | 3,691888 |
| 6 | 5,1 | 9,1 | -2,629 | 1,979 | -5,20082 | 6,909388 | 3,914745 |
| 7 | 6 | 7 | -1,729 | -0,121 | 0,209898 | 2,987959 | 0,014745 |
| 8 | 10,2 | 5,1 | 2,471 | -2,021 | -4,99582 | 6,107959 | 4,086173 |
| 9 | 8,2 | 6 | 0,471 | -1,121 | -0,52867 | 0,222245 | 1,257602 |
| 10 | 5,6 | 10,2 | -2,129 | 3,079 | -6,55296 | 4,530816 | 9,477602 |
| 11 | 6,4 | 8,2 | -1,329 | 1,079 | -1,43296 | 1,765102 | 1,163316 |
| 12 | 10,8 | 5,6 | 3,071 | -1,521 | -4,67296 | 9,433673 | 2,314745 |
| 13 | 9,1 | 6,4 | 1,371 | -0,721 | -0,98939 | 1,880816 | 0,520459 |
| 14 | 6,7 | 10,8 | -1,029 | 3,679 | -3,78367 | 1,057959 | 13,53189 |
| 15 | 7,5 | 9,1 | -0,229 | 1,979 | -0,45224 | 0,052245 | 3,914745 |
| 16 | 11,3 | 6,7 | 3,571 | -0,421 | -1,5051 | 12,7551 | 0,177602 |
| Итого | 108,2 | 99,7 | - | - | -27,9786 | 56,50857 | 52,24357 |
Выборочные средние:
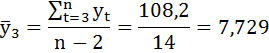
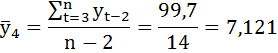
Коэффициент автокорреляции уровней ряда первого порядка:
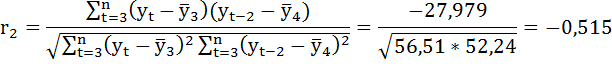
Продолжив расчёты аналогичным образом, получим автокорреляционную функцию этого ряда. Её значения приведены в таблице:
| Лаг | Коэффициент автокорреляции уровней |
|---|---|
| 1 | 0,1917 |
| 2 | -0,5149 |
| 3 | 0,1272 |
| 4 | 0,9862 |
| 5 | 0,1448 |
| 6 | -0,6487 |
| 7 | -0,00647 |
| 8 | 0,9632 |
Анализ значений автокорреляционной функции позволяет сделать вывод о наличии в изучаемом временном ряде линейной тенденции и сезонных колебаний периодичностью в 4 квартала.
2. Построим аддитивную модель временного ряда.
Общий вид аддитивной модели следующий:
Y = T + S + E
Эта модель предполагает, что каждый уровень временного ряда может быть представлен как сумма трендовой (T), сезонной (S) и случайной (E) компонент.
Рассчитаем компоненты аддитивной модели временного ряда.
Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого:
1) просуммируем уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент времени и определим условные годовые объёмы потребления электроэнергии (гр. 3);
2) разделив полученные суммы на 4, найдём скользящие средние (гр. 4). Отметим, что полученные таким образом выравненные значения уже не содержат сезонной компоненты;
3) приведём эти значения в соответствие с фактическими моментами времени, для чего найдём средние значения из двух последовательных скользящих средних – центрированные скользящие средние (гр.5).
Расчёт оценок сезонной компоненты в аддитивной модели
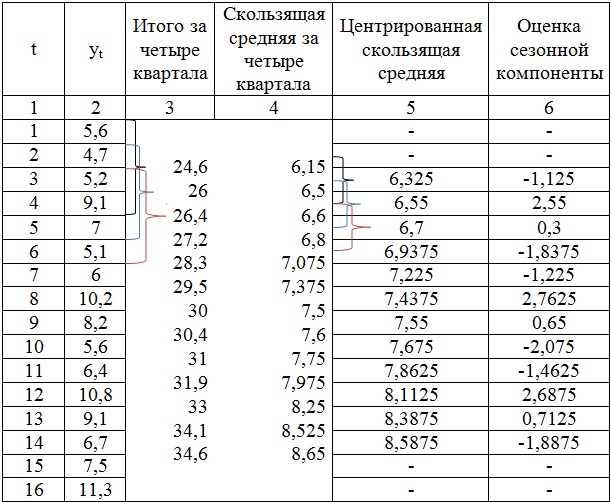
Шаг 2. Рассчитаем оценки сезонной компоненты как разность между фактическими уровнями ряда и центрированными скользящими средними (гр. 6). Используем эти оценки для расчета значений сезонной компоненты S. Для этого найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты Si. В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю.
Расчёт значений сезонной компоненты:
| Показатели | Год | № квартала, i | |||
|---|---|---|---|---|---|
| I | II | III | IV | ||
| 1 | - | - | -1,125 | 2,55 | |
| 2 | 0,3 | -1,8375 | -1,225 | 2,7625 | |
| 3 | 0,65 | -2,075 | -1,4625 | 2,6875 | |
| 4 | 0,7125 | -1,8875 | - | - | |
| Итого за i-й квартал | 1,6625 | -5,8 | -3,8125 | 8 | |
Средняя оценка сезонной компоненты для i-го квартала, 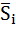 |
0,554167 | -1,93333 | -1,27083 | 2,666667 | |
| Скорректированная сезонная компонента, Si | 0,55 | -1,9375 | -1,275 | 2,6625 | |
Для данной модели имеем:
0,554167 + ( -1,93333) + (-1,27083) + 2,666667 = 0,016667
Определим корректирующий коэффициент:
k = 0,016667 / 4 = 0,004167
Рассчитаем скорректированные значения сезонной компоненты как разность между её средней оценкой и корректирующим коэффициентом k:
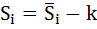
Проверим условие равенство нулю суммы значений сезонной компоненты:
0,55 + (-1,9375) + (-1,275) + 2,6625 = 0
Таким образом, получены следующие значения сезонной компоненты:
I квартал: S1 = 0,55;
II квартал: S2 = -1,9375;
III квартал: S3 = -1,275;
IV квартал: S4 = 2,6625.
Занесём полученные значения в таблицу для соответствующих кварталов каждого года (гр. 3).
| t | yt | Si | T + E = yt – Si | T | T + S | E = yt – (T + S) | E2 |
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 5,6 | 0,55 | 5,05 | 5,8588235 | 6,408824 | -0,80882 | 0,654196 |
| 2 | 4,7 | -1,9375 | 6,6375 | 6,0651471 | 4,127647 | 0,572353 | 0,327588 |
| 3 | 5,2 | -1,275 | 6,475 | 6,2714706 | 4,996471 | 0,203529 | 0,041424 |
| 4 | 9,1 | 2,6625 | 6,4375 | 6,4777941 | 9,140294 | -0,04029 | 0,001624 |
| 5 | 7 | 0,55 | 6,45 | 6,6841176 | 7,234118 | -0,23412 | 0,054811 |
| 6 | 5,1 | -1,9375 | 7,0375 | 6,8904412 | 4,952941 | 0,147059 | 0,021626 |
| 7 | 6 | -1,275 | 7,275 | 7,0967647 | 5,821765 | 0,178235 | 0,031768 |
| 8 | 10,2 | 2,6625 | 7,5375 | 7,3030882 | 9,965588 | 0,234412 | 0,054949 |
| 9 | 8,2 | 0,55 | 7,65 | 7,5094118 | 8,059412 | 0,140588 | 0,019765 |
| 10 | 5,6 | -1,9375 | 7,5375 | 7,7157353 | 5,778235 | -0,17824 | 0,031768 |
| 11 | 6,4 | -1,275 | 7,675 | 7,9220588 | 6,647059 | -0,24706 | 0,061038 |
| 12 | 10,8 | 2,6625 | 8,1375 | 8,1283824 | 10,79088 | 0,009118 | 8,31E-05 |
| 13 | 9,1 | 0,55 | 8,55 | 8,3347059 | 8,884706 | 0,215294 | 0,046352 |
| 14 | 6,7 | -1,9375 | 8,6375 | 8,5410294 | 6,603529 | 0,096471 | 0,009307 |
| 15 | 7,5 | -1,275 | 8,775 | 8,7473529 | 7,472353 | 0,027647 | 0,000764 |
| 16 | 11,3 | 2,6625 | 8,6375 | 8,9536765 | 11,61618 | -0,31618 | 0,099968 |
Шаг 3. Исключим влияние сезонной компоненты, вычитая ее значение из каждого уровня исходного временного ряда. Получим величины T + E = Y - S (гр. 4 табл.). Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту.
Шаг 4. Определим компоненту T данной модели. Для этого проведем аналитическое выравнивание ряда (T + E) с помощью линейного тренда. Результаты аналитического выравнивания следующие:
T = 5,6525 + 0,206 * t
Подставляя в это уравнение значения t = 1,...,16, найдем уровни T для каждого момента времени (гр. 5 табл.).
Шаг 5. Найдем значения уровней ряда, полученные по аддитивной модели. Для этого прибавим к уровням T значения сезонной компоненты для соответствующих кварталов (гр. 6 табл.).
Для оценки качества построенной модели применим сумму квадратов полученных абсолютных ошибок.
Коэффициент детерминации.
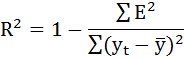
| t | yt | Е2 | 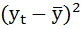 |
|---|---|---|---|
| 1 | 5,6 | 0,654196 | 3,262539 |
| 2 | 4,7 | 0,327588 | 7,323789 |
| 3 | 5,2 | 0,041424 | 4,867539 |
| 4 | 9,1 | 0,001624 | 2,868789 |
| 5 | 7 | 0,054811 | 0,165039 |
| 6 | 5,1 | 0,021626 | 5,318789 |
| 7 | 6 | 0,031768 | 1,977539 |
| 8 | 10,2 | 0,054949 | 7,805039 |
| 9 | 8,2 | 0,019765 | 0,630039 |
| 10 | 5,6 | 0,031768 | 3,262539 |
| 11 | 6,4 | 0,061038 | 1,012539 |
| 12 | 10,8 | 8,31E-05 | 11,51754 |
| 13 | 9,1 | 0,046352 | 2,868789 |
| 14 | 6,7 | 0,009307 | 0,498789 |
| 15 | 7,5 | 0,000764 | 0,008789 |
| 16 | 11,3 | 0,099968 | 15,16129 |
| Итого | 118,5 | 1,457029 | 68,549 |
Рассчитаем коэффициент детерминации.
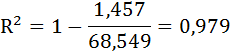
Следовательно, можно сказать, что аддитивная модель объясняет 97,9% общей вариации уровней временного ряда.
Далее необходимо провести проверку адекватности модели данным наблюдения. Воспользуемся F-критерием Фишера:
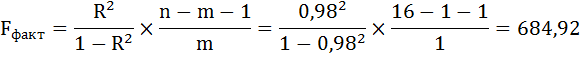
где m - количество факторов в уравнении тренда (m=1).
Табличное значение F-критерия Фишера при уровне значимости α = 0,05,
k1 = m = 1, k2 = n - m - 1 = 14,
Fтабл = 4,60
Поскольку F > Fтабл, то уравнение статистически значимо, надёжно.
Шаг 6. Прогнозирование по аддитивной модели.
Прогнозное значение Ft уровня временного ряда в аддитивной модели есть сумма трендовой и сезонной компонент. Для определения трендовой компоненты воспользуемся уравнением тренда:
T = 5,6525 + 0,206 × t
Прогноз на 1 период:
T17 = 5,6525 + 0,206 × 17 = 9,16
Значение сезонного компонента за соответствующий период равно:
S1 = 0,55
Таким образом,
F17 = T17 + S1 = 9,16 + 0,55 = 9,71
Прогноз на 2 период:
T18 = 5,6525 + 0,206 × 18 = 9,366
Значение сезонной компоненты за соответствующий период равно:
S2 = – 1,9375
Таким образом, прогнозное значение на 2 квартала вперёд составит:
F18 = T18 + S2 = 9,366 – 1,9375 = 7,429
Смотри ещё
- Выборочное наблюдение / Задача №32. Расчёт предела, в котором находится средний возраст рабочих
- Выборочное наблюдение / Задача №33. Расчёт предела, в котором находится средняя крепость пряжи в партии
- Выборочное наблюдение / Задача №39. Расчёт предела, в котором находятся средние затраты времени
- Эконометрика / Задача №1 Построение уравнения регрессии
- Эконометрика / Задача №3. Расчёт параметров регрессии и корреляции с помощью Excel
- Эконометрика / Задача №4. Построение регрессионной модели с использованием фиктивной переменной























