Задача №45. Расчёт абсолютных и относительных показателей вариации
Имеются следующие данные выборочного обследования студентов одного из вузов:
| Затраты времени на дорогу до института, час | Число студентов, % к итогу |
|---|---|
| До 0,5 | 7 |
| 0,5 – 1,0 | 18 |
| 1,0 – 1,5 | 32 |
| 1,5 – 2,0 | 37 |
| Свыше 2,0 | 6 |
| Всего | 100 |
Вычислите абсолютные и относительные показатели вариации.
Решение:
Проанализируем исходные данные.
Данный ряд распределения содержит открытые интервалы, которые предварительно необходимо закрыть. Величина интервала второй группы равна 0,5 следовательно, и величина первой группы также равна 0,5. Величина интервала предпоследней группы равна 0,5, значит, и последний интервал будет иметь величину, равную 0,5.
Найдём абсолютные показатели вариации:
1) Определим размах вариации как разность между наибольшим и наименьшим значением признака:
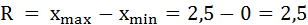
Размах вариации затрат времени на дорогу до института равен 2,5 часа.
2) Средние затраты времени определим по формуле средней арифметической взвешенной.
Предварительно определим дискретную величину признака в каждом интервале. Для этого по формуле средней арифметической простой найдём середины интервалов.
Среднее значение первого интервала будет равно:
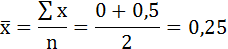
Занесём результаты вычислений в таблицу:
| Затраты времени на дорогу до института, час | Закрытые интервалы | Середина интервала, (х) | Число студентов, % к итогу, (f) | хf |
|---|---|---|---|---|
| До 0,5 | 0 – 0,5 | 0,25 | 7 | 1,75 |
| 0,5 – 1,0 | 0,5 – 1,0 | 0,75 | 18 | 13,5 |
| 1,0 – 1,5 | 1,0 – 1,5 | 1,25 | 32 | 40 |
| 1,5 – 2,0 | 1,5 – 2,0 | 1,75 | 37 | 64,75 |
| Свыше 2,0 | 2,0 – 2,5 | 2,25 | 6 | 13,5 |
| Всего | – | – | 100 | 133,5 |
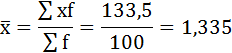
3) Среднее линейное отклонение есть средняя арифметическая из абсолютных отклонений отдельных значений признака от общей средней:
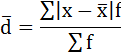
| Затраты времени на дорогу до института, час | Середина интервала, (х) | Число студентов, % к итогу, (f) | хf | 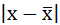 |
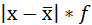 |
|---|---|---|---|---|---|
| До 0,5 | 0,25 | 7 | 1,75 | 1,085 | 7,595 |
| 0,5 – 1,0 | 0,75 | 18 | 13,5 | 0,585 | 10,53 |
| 1,0 – 1,5 | 1,25 | 32 | 40 | 0,085 | 2,72 |
| 1,5 – 2,0 | 1,75 | 37 | 64,75 | 0,415 | 15,355 |
| Свыше 2,0 | 2,25 | 6 | 13,5 | 0,915 | 4,49 |
| Всего | - | 100 | 133,5 | - | 41,69 |
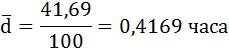
Среднее линейное отклонение затрат времени составляет 0,4169 часа.
4) Дисперсия - это средняя арифметическая квадратов отклонений каждого значения признака от средней арифметической.
Расчёт дисперсии в интервальных рядах распределения производится по формуле:
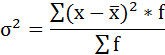
Построим вспомогательную таблицу:
| Затраты времени на дорогу до института, час | Середина интервала, (х) | Число студентов, % к итогу, (f) | 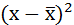 |
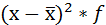 |
|---|---|---|---|---|
| До 0,5 | 0,25 | 7 | 1,17723 | 8,24058 |
| 0,5 – 1,0 | 0,75 | 18 | 0,34223 | 6,16005 |
| 1,0 – 1,5 | 1,25 | 32 | 0,00722 | 0,2312 |
| 1,5 – 2,0 | 1,75 | 37 | 0,17223 | 6,37233 |
| Свыше 2,0 | 2,25 | 6 | 0,83723 | 5,02335 |
| Всего | - | 100 | 2,53613 | 26,0275 |
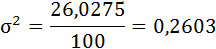
5) Среднее квадратическое отклонение затрат времени определяется как корень квадратный из дисперсии:
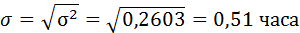
Найдём относительные показатели вариации:
6) Коэффициент вариации - это отношение среднего квадратического отклонения к средней арифметической:
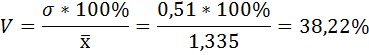
По величине коэффициента вариации можно судить о степени вариации признаков совокупности. Чем больше его величина, тем больше разброс значения признаков вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя.
Поскольку V > 33%, следовательно, вариация значительная, а совокупность не однородна.
7) Коэффициент осцилляции отражает относительную колеблемость крайних значений признака вокруг средней и определяется по формуле:
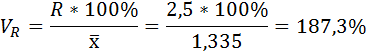
8) Относительное линейное отклонение:
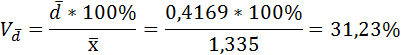
Смотри ещё
- Анализ хозяйственной деятельности / Задача №2. Анализ ритмичности работы предприятия
- Выборочное наблюдение / Задача №32. Расчёт предела, в котором находится средний возраст рабочих
- Выборочное наблюдение / Задача №39. Расчёт предела, в котором находятся средние затраты времени
- Основные макроэкономические показатели / Задача №21. Расчёт индекса-дефлятора ВВП
- Средние величины и показатели вариации / Задача №1. Расчёт средней арифметической, модального и медианного значения
- Средние величины и показатели вариации / Задача №3. Расчёт среднего времени
- Средние величины и показатели вариации / Задача №4. Расчёт средней заработной платы
- Средние величины и показатели вариации / Задача №5. Расчёт средней арифметической взвешенной в интервальном ряду распределения
- Средние величины и показатели вариации / Задача №6. Расчёт показателей вариации
- Средние величины и показатели вариации / Задача №7. Расчёт коэффициента вариации
- Средние величины и показатели вариации / Задача №9. Расчёт среднего квадрата индивидуальных значений признака
- Средние величины и показатели вариации / Задача №10. Расчёт среднего квадрата отклонений вариантов признака от произвольной величины
- Средние величины и показатели вариации / Задача №12. Расчёт коэффициента вариации
- Средние величины и показатели вариации / Задача №13. Расчёт среднего квадрата отклонений индивидуальных значений признака от произвольной величины
- Средние величины и показатели вариации / Задача №22. Виды дисперсии и их расчёт
- Средние величины и показатели вариации / Задача №23. Расчёт показателей асимметрии и эксцесса
- Средние величины и показатели вариации / Задача №24. Расчёт показателей вариации по несгруппированным данным
- Средние величины и показатели вариации / Задача №26. Расчёт среднего удоя
- Средние величины и показатели вариации / Задача №27. Расчёт средней себестоимости
- Средние величины и показатели вариации / Задача №28. Расчёт среднего процента выполнения плана выпуска продукции
- Средние величины и показатели вариации / Задача №29. Расчёт крайних значений вариационного ряда
- Средние величины и показатели вариации / Задача №30. Расчёт коэффициента вариации
- Средние величины и показатели вариации / Задача №43. Расчёт описательных статистик
- Средние величины и показатели вариации / Задача №48. Расчёт показателей вариации
- Статистика населения / Задача №2. Расчёт средней численности населения
- Статистика населения / Задача №3. Расчёт средней численности населения
- Статистика населения / Задача №11. Расчёт коэффициентов брачности и разводимости
- Статистические методы изучения взаимосвязей / Задача №47. Построение модели линейной регрессии
- Эконометрика / Задача №1 Построение уравнения регрессии
- Эконометрика / Задача №4. Построение регрессионной модели с использованием фиктивной переменной























