Задача №4. Построение регрессионной модели с использованием фиктивной переменной
Исследовать зависимость между результатами зимней (Х) и летней (У) сессий.
В таблице приведена средняя оценка, полученная по итогам сессии, а также указана принадлежность студента к группе А или Б.
| № п/п | х | у | Группа |
|---|---|---|---|
| 1 | 3,7 | 4,8 | Б |
| 2 | 3,5 | 3,5 | Б |
| 3 | 4,3 | 5 | Б |
| 4 | 3 | 4 | Б |
| 5 | 4,6 | 4,2 | Б |
| 6 | 4,6 | 4,1 | Б |
| 7 | 3,8 | 4,8 | А |
| 8 | 3,6 | 3,5 | Б |
| 9 | 3,3 | 4,4 | Б |
| 10 | 3,9 | 3 | Б |
| 11 | 4,7 | 3,7 | Б |
| 12 | 4,6 | 4,4 | Б |
| 13 | 4,6 | 3,8 | Б |
| 14 | 3,3 | 3,1 | Б |
| 15 | 4,3 | 3,6 | Б |
| 16 | 3,1 | 4,8 | А |
| 17 | 3,2 | 3 | А |
| 18 | 4,2 | 4,8 | А |
| 19 | 3,3 | 3,4 | Б |
| 20 | 3,5 | 4,2 | А |
1. Построить линейную регрессионную модель У по Х.
2. Проверить значимость коэффициентов уравнения и самого уравнения регрессии.
3. Построить регрессионную модель У по Х с использованием фиктивной переменной «группа».
4. Проверить значимость коэффициентов уравнения и самого уравнения регрессии.
5. Вычислить коэффициенты детерминации для обычной модели и модели с фиктивной переменной.
Решение:
1. Для расчёта параметров а и b линейной регрессии
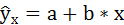
необходимо решить систему нормальных уравнений относительно a и b:
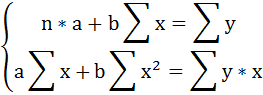
Число наблюдений n = 20.
Построим таблицу исходных и расчётных данных.
Таблица 1 Расчетные данные для оценки линейной регрессии
| № п/п | х | у | х2 | у2 | х*у | 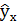 |
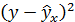 |
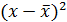 |
Группа | z |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3,7 | 4,8 | 13,69 | 23,04 | 17,76 | 3,973 | 0,684 | 0,024 | Б | 1 |
| 2 | 3,5 | 3,5 | 12,25 | 12,25 | 12,25 | 3,931 | 0,186 | 0,126 | Б | 1 |
| 3 | 4,3 | 5 | 18,49 | 25 | 21,5 | 4,098 | 0,814 | 0,198 | Б | 1 |
| 4 | 3 | 4 | 9 | 16 | 12 | 3,827 | 0,030 | 0,731 | Б | 1 |
| 5 | 4,6 | 4,2 | 21,16 | 17,64 | 19,32 | 4,160 | 0,002 | 0,555 | Б | 1 |
| 6 | 4,6 | 4,1 | 21,16 | 16,81 | 18,86 | 4,160 | 0,004 | 0,555 | Б | 1 |
| 7 | 3,8 | 4,8 | 14,44 | 23,04 | 18,24 | 3,994 | 0,650 | 0,003 | А | 0 |
| 8 | 3,6 | 3,5 | 12,96 | 12,25 | 12,6 | 3,952 | 0,204 | 0,065 | Б | 1 |
| 9 | 3,3 | 4,4 | 10,89 | 19,36 | 14,52 | 3,889 | 0,261 | 0,308 | Б | 1 |
| 10 | 3,9 | 3 | 15,21 | 9 | 11,7 | 4,014 | 1,029 | 0,002 | Б | 1 |
| 11 | 4,7 | 3,7 | 22,09 | 13,69 | 17,39 | 4,181 | 0,232 | 0,714 | Б | 1 |
| 12 | 4,6 | 4,4 | 21,16 | 19,36 | 20,24 | 4,160 | 0,057 | 0,555 | Б | 1 |
| 13 | 4,6 | 3,8 | 21,16 | 14,44 | 17,48 | 4,160 | 0,130 | 0,555 | Б | 1 |
| 14 | 3,3 | 3,1 | 10,89 | 9,61 | 10,23 | 3,889 | 0,623 | 0,308 | Б | 1 |
| 15 | 4,3 | 3,6 | 18,49 | 12,96 | 15,48 | 4,098 | 0,248 | 0,198 | Б | 1 |
| 16 | 3,1 | 4,8 | 9,61 | 23,04 | 14,88 | 3,848 | 0,907 | 0,570 | А | 0 |
| 17 | 3,2 | 3 | 10,24 | 9 | 9,6 | 3,868 | 0,754 | 0,429 | А | 0 |
| 18 | 4,2 | 4,8 | 17,64 | 23,4 | 20,16 | 4,077 | 0,523 | 0,119 | А | 0 |
| 19 | 3,3 | 3,4 | 10,89 | 11,56 | 11,22 | 3,889 | 0,239 | 0,308 | Б | 1 |
| 20 | 3,5 | 4,2 | 12,25 | 17,64 | 14,7 | 3,930 | 0,072 | 0,126 | А | 0 |
| Итого: | 77,1 | 80,1 | 303,67 | 328,73 | 310,13 | 80,1 | 7,649 | 6,45 | х | 15 |
| Среднее: | 3,855 | 4,005 | 15,184 | 16,4365 | 15,5065 | х | х | х | х | х |
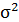 |
0,322 | 0,396 | х | х | х | х | х | х | х | х |
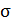 |
0,568 | 0,630 | х | х | х | х | х | х | х | х |
Среднее значение определим по формуле:
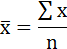
Среднее квадратическое отклонение рассчитаем по формуле:
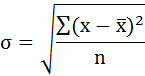
Возведя в квадрат полученное значение, получим дисперсию:
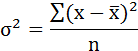
Параметры уравнения можно определить также и по формулам:
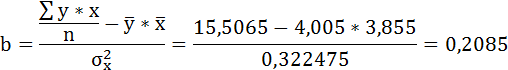
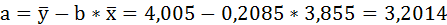
Таким образом, уравнение регрессии имеет вид:
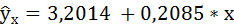
Следовательно, с повышением средней оценки, полученной по итогам зимней сессии, на один балл, средняя оценка по итогам летней сессии увеличивается в среднем на 0,2085.
2. Рассчитаем линейный коэффициент парной корреляции:
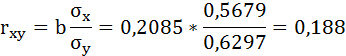
Связь очень слабая, практически отсутствует.
Определим коэффициент детерминации:
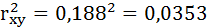
Вариация результата на 3,53% объясняется вариацией фактора х. На долю других, не учтённых в модели факторов, приходится 96,47%. Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчётные) значения 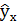 .
.
Так как 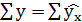 , следовательно, параметры уравнения определены верно.
, следовательно, параметры уравнения определены верно.
3. Проверим значимость коэффициентов уравнения и самого уравнения регрессии.
Оценку качества уравнения регрессии проведём с помощью F-критерия Фишера.
F-критерий состоит в проверке гипотезы Н0 о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт и критического (табличного) Fтабл значений F-критерия Фишера.
Fфакт определяется по формуле:
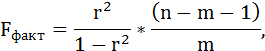
где n – число единиц совокупности;
m – число параметров при переменных х.
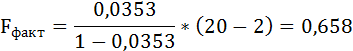
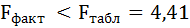
Таким образом, Н0 – гипотеза о случайной природе оцениваемых характеристик принимается и признаётся их статистическая незначимость и ненадёжность.
4. Оценку статистической значимости коэффициентов регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительного интервала каждого из показателей.
Выдвигаем гипотезу Н0 о статистически незначимом отличии показателей от нуля: a = b = rxy = 0.
tтабл = 2,1 для числа степеней свободы df = n – 2 = 18 и α = 0,05.
Определим случайные ошибки ma, mb, mrxy:
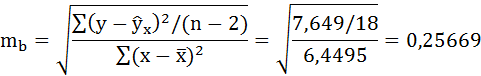
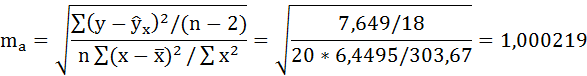
Фактические значения t-статистики определим по формулам:
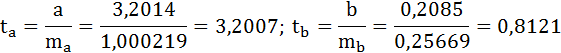
t-критерий для коэффициента корреляции можно рассчитать двумя способами:
1) 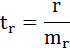
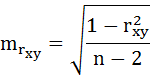 – случайная ошибка коэффициента корреляции.
– случайная ошибка коэффициента корреляции.
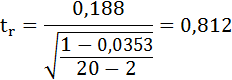
2) Кроме того
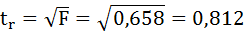
Сравним фактические значения t-статистики с табличными значениями.
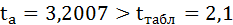
Так как фактическое значение t-критерия для коэффициента а превышает табличное, следовательно, гипотезу о несущественности коэффициента а можно отклонить.
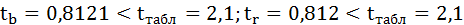
Величина t-критерия для коэффициента регрессии меньше табличного и совпадает с величиной tr.
Следовательно, полученная линейная зависимость является недостоверной.
5. По 20 наблюдениям уравнение линейной регрессии (без учёта принадлежности студента к группе А или Б) составило:
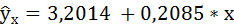
Введём в уравнение регрессии фиктивную переменную z для отражения принадлежности студента к группе, а именно: z = 1, для группы Б и z = 0 для группы А. Уравнение регрессии примет вид:
уxz = a + b*x + c*z + ɛ
Применяя метод наименьших квадратов для оценки параметров данного уравнения, получим следующую систему нормальных уравнений:
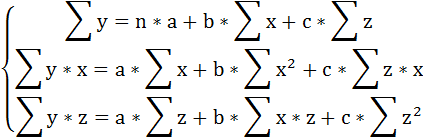
В виду того, что z принимает лишь два значения (1 и 0), Σz = n1 = 15 (число студентов группы Б), Σх*z =Σх1 =59,3 (сумма х по группе Б), Σz2 =Σz =15, Σy*z =Σy1 =58,5 (сумма у по группе Б).
Тогда система нормальных уравнений примет вид:
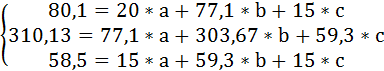
Решая её, получим уравнение регрессии:
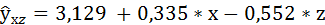
6. Найдём индекс детерминации для данной модели по формуле:
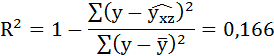
Добавление в регрессию фиктивной переменной существенно улучшило результат модели: доля объяснённой вариации выросла с 3,53% (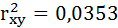 ) до 16,6% (Rухz2 = 0,166). Но, не смотря на это, связь между признаками остаётся слабой.
) до 16,6% (Rухz2 = 0,166). Но, не смотря на это, связь между признаками остаётся слабой.
7. Значимость уравнения множественной регрессии в целом, так же как и в парной регрессии, оценивается с помощью F-критерия Фишера:
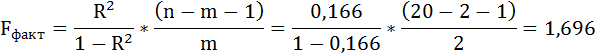
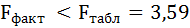
Так как фактическое значение F-критерия меньше табличного, то уравнение статистически не значимо.
8. Оценка значимости коэффициентов регрессии производится, как и в парной регрессии по t-критерию Стьюдента, по формуле:
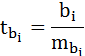
где bi – величина параметра регрессии (в наших обозначениях это a, b и с)
a = 3,129; b = 0,335; с = - 0,5516;
ma = 0,9578; mb = 0,2574; mc = 0,3376;
ta = 3,266; tb = 1,3; tc = -1,634.
Величина t-статистики коэффициентов регрессии b и c меньше табличного tтабл.=2,1 при уровне значимости α 0,05, что свидетельствует о случайной природе взаимосвязи, о статистической ненадёжности всего уравнения.
Таким образом, уравнение в целом незначимо и ненадёжно и не может использоваться в дальнейшем для анализа и прогноза.

Экономическая прибыль

Счёт операций с капиталом
Смотри ещё
- Выборочное наблюдение / Задача №39. Расчёт предела, в котором находятся средние затраты времени
- Средние величины и показатели вариации / Задача №6. Расчёт показателей вариации
- Средние величины и показатели вариации / Задача №7. Расчёт коэффициента вариации
- Средние величины и показатели вариации / Задача №9. Расчёт среднего квадрата индивидуальных значений признака
- Средние величины и показатели вариации / Задача №10. Расчёт среднего квадрата отклонений вариантов признака от произвольной величины
- Средние величины и показатели вариации / Задача №12. Расчёт коэффициента вариации
- Средние величины и показатели вариации / Задача №13. Расчёт среднего квадрата отклонений индивидуальных значений признака от произвольной величины
- Средние величины и показатели вариации / Задача №22. Виды дисперсии и их расчёт
- Средние величины и показатели вариации / Задача №23. Расчёт показателей асимметрии и эксцесса
- Средние величины и показатели вариации / Задача №24. Расчёт показателей вариации по несгруппированным данным
- Средние величины и показатели вариации / Задача №29. Расчёт крайних значений вариационного ряда
- Средние величины и показатели вариации / Задача №30. Расчёт коэффициента вариации
- Средние величины и показатели вариации / Задача №43. Расчёт описательных статистик
- Средние величины и показатели вариации / Задача №45. Расчёт абсолютных и относительных показателей вариации
- Средние величины и показатели вариации / Задача №48. Расчёт показателей вариации
- Статистические методы изучения взаимосвязей / Задача №47. Построение модели линейной регрессии
- Статистические методы изучения взаимосвязей / Задача №53. Расчёт точечного прогноза
- Эконометрика / Задача №1 Построение уравнения регрессии
- Эконометрика / Задача №3. Расчёт параметров регрессии и корреляции с помощью Excel
- Эконометрика / Задача №5. Построение автокорреляционной функции

Счёт использования располагаемого дохода




















