Общий доход

Найти максимум прибыли монополиста, если известно, что спрос на его продукцию описывается функцией:

Q = 165 - 0,5 × P

и функция общих затрат равна:

TC = 5500 + 30 × Q + Q²

Решение

Функция спроса на продукцию монополиста

Q = 110 - 0,5 × P

и функция общих затрат

ТС = 1500 + 40 × Q + Q².

Найти объём производства, обеспечивающий максимальную прибыль. Вычислить наибольшую прибыль.

Решение

Монополия на рынке имеет следующую функцию предельных издержек:

МС = - 10 + 3 × Q.

Предельный доход выражен функцией:

MR = 40 - 2 × Q.

Какова цена, назначаемая монополией за свой продукт на рынке?

Решение

Даны функция спроса на продукцию монополиста

Q = 25 - P

и функция средних переменных затрат

AVC = 4 + 0,5 × Q.

Известно, что максимум прибыли монополиста равен 23,5. Найти его фиксированные затраты.

Решение

Даны функция спроса на продукцию монополиста

Q = 26 - 0,5 × P

и функция общих затрат

ТС = 120 - 8 × Q + Q².

Найти максимальную прибыль и соответствующую цену.

Решение

Функция спроса на продукцию монополиста:

P = 20 - 2 × Q,

MC = AC = 4.

Найти эластичность спроса по цене, если монополист ищет максимум прибыли.

Решение

Известна функция спроса на продукцию монополиста

Q = 220 - 4 × P,

и дана функция предельных затрат

MC = 10 + 4 × Q.

Известно, что максимум прибыли монополиста равен 125. Найти его фиксированные затраты.

Решение

По данным исследования рынка, кривая спроса представляет собой отрезок прямой, а величина спроса при цене, равной 5 р. за штуку, составляет 300 тыс. штук в год и падает на 30 тыс. штук при увеличении цены на каждый рубль. Какую цену выгодно установить монополисту, если постоянные издержки составляют 150 тыс. р. в год, переменные затраты на единицу товара равны 3 р.?

Решение

Допустим, общие затраты монополии равны

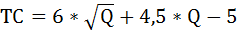
при спросе на её продукцию

Q = 32 – 4 × Р.

Найти оптимальную цену и выпуск продукции, обеспечивающие наибольшую прибыль. Вычислить эту прибыль.

Решение

Переменные затраты зависят от выпуска следующим образом:

VC = Q.

Постоянные затраты составляют 100. Предельная выручка монополиста зависит от объёма продаж как

MR = 49 – Q.

Найти монопольную цену и коэффициент Лернера.

Решение