Задача №20. Расчёт текущей стоимости облигации
Определить текущую стоимость муниципальной облигации из портфеля ценных бумаг коммерческого банка.
Номинальная стоимость облигации 300 тыс. руб.
До погашения четыре года.
Годовая ставка купонного дохода по облигации соответственно: 5%, 6%, 6%, 7%.
Рыночная процентная ставка – 8% в год.
Решение:
Текущую стоимость облигации можно определить как стоимость ожидаемого денежного потока, приведённого к текущему моменту времени. Денежный поток состоит из двух компонентов: купонных выплат и наминала облигации, выплачиваемого при её погашении. То есть, цена облигации будет равна приведённой стоимости аннуитета и единовременно выплачиваемой суммы номинальной стоимости.
Формула расчёта текущей стоимости облигации будет следующей:
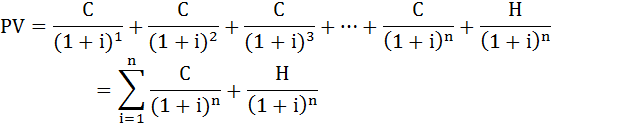
где
C – купонные выплаты;
i – рыночная процентная ставка в период t (доходность в альтернативные финансовые инструменты);
H – номинальная стоимость облигации;
n – число периодов, в течении которых осуществляется выплата купонного дохода.
Рассчитаем купонные выплаты. Абсолютная величина годовой доходности рассчитывается по формуле:
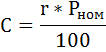
где
r – годовая ставка купонного дохода по облигации, %;
Рном – номинальная стоимость облигации.
Купонная выплата за первый год:
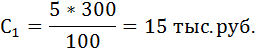
Купонная выплата за второй и третий год:
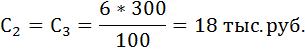
Купонная выплата за четвёртый год:
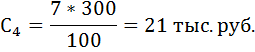
Таким образом, текущая стоимость муниципальной облигации из портфеля ценных бумаг коммерческого банка будет равна:
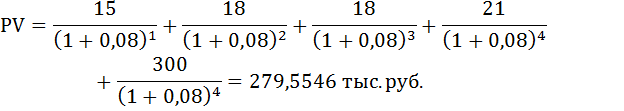
Смотри ещё
- Макроэкономическая нестабильность / Задача №33. Расчёт реального дохода вкладчика с учётом инфляции
- Провалы рынка и государственное регулирование / Задача №194. Расчёт общественно оптимального уровня производства фирмы
- Рынки факторов производства / Задача №161. Выбор проекта для инвестирования
- Рынки факторов производства / Задача №184. Купить или арендовать?
- Финансовая математика / Задача №1. Расчёт наращенной суммы долга
- Финансовая математика / Задача №3. Рассчёт суммы долга с процентами при сроке менее года
- Финансовая математика / Задача №10. Расчёт NPV и PI
- Финансовая математика / Задача №11. Расчёт текущей стоимости облигации
- Финансовая математика / Задача №12. Расчёт текущей стоимости обыкновенной акции
- Финансовая математика / Задача №15. Определение целесообразности скидки
- Финансовая математика / Задача №18. Расчёт наращенной суммы вклада
- Финансовая математика / Задача №21. Расчёт срока наращения
- Финансовая математика / Задача №22. Расчёт суммы, полученной владельцем векселя при учете
- Финансовая математика / Задача №23. Расчёт учётной ставки
- Финансовая математика / Задача №24. Сравнение вариантов наращения
- Финансовая математика / Задача №25. Расчёт общего дохода банка от операции вексельного учёта
- Финансовая математика / Задача №26. Расчёт ставки процентов по кредиту с учетом инфляции
- Финансовая математика / Задача №30. Расчёт наращенной суммы вклада
- Финансовая математика / Задача №32. Расчёт текущей стоимости актива
- Фискальная политика / Задача №47. Расчёт суммы налога
- Фискальная политика / Задача №48. Расчёт суммы налога
- Экономика предприятия / Задача №26. Оценка доходности инвестиций в предприятие























