Задача №33. Расчёт предела, в котором находится средняя крепость пряжи в партии

В порядке механической выборки было под­вергнуто испытанию на разрыв 100 нитей из партии. В результате обследования установлена средняя кре­пость пряжи 320 г при среднем квадратическом откло­нении 20 г. С вероятностью 0,954 определите предел, в котором находится средняя крепость пряжи в партии.

Решение:

По условию задачи средняя кре­пость пряжи:

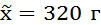
1. Рассчитаем дисперсию выборочной совокупности:

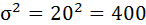
2. Рассчитаем среднюю   ошибку выборочной   средней:

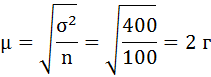
3. С вероятностью 0, 954 рассчитаем предельную ошибку выборочной  средней.

При   Р = 0,954, t = 2,0 (другие значения t можно посмотреть в Задаче №32):

Δ = μ * t = 2 * 2 = 4 г.

4. Определим пределы, в которых находится средняя крепость пряжи в партии.

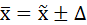
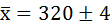
Генеральная средняя ( 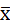) находится в пределах:

320 – 4 ˂ 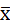˂ 320 + 4.

316 ˂ 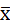˂ 324

С вероятностью 0,954 можно утверждать, что средняя крепость пряжи в партии находится в пределах 316 ˂ 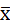˂ 324 г.