Задача №15. Расчёт валового выпуска на основе уравнения математической модели МОБ
Имеются две отрасли экономики. Данные о коэффициентах прямых затрат (матрица размерностью 2х2) и конечном спросе по каждой отрасли, соответственно Yi, представлены в таблице:
| Коэффициенты прямых затрат, aij | Конечный спрос, Yi | |
|---|---|---|
| а11=0,27 | а12=0,35 | Y1=800 |
| а21=0,63 | а22=0,45 | Y2=200 |
Определите:
1) валовой выпуск по экономике в целом (Х1 + Х2) и соотношение валового выпуска и ВВП, а также ВВП и промежуточного потребления;
2) повышение экономической эффективности производства (по показателю затратоёмкости ВВП, равному соотношению стоимости потреблённых в процессе производства продуктов и услуг к объёму ВВП), если прямые затраты первой продукции на производство единицы второй продукции уменьшатся на 20%.
Примечание: Для расчетов необходимо построить два уравнения: уравнение по первой строке и уравнение по второй строке балансовой таблицы, используя уравнение математической модели межотраслевого баланса. Вопросы различий в оценке выпуска (валового выпуска) и ВВП здесь не рассматриваются.
Решение:
Уравнение математической модели межотраслевого баланса в общем виде имеет вид:
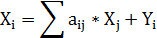
где
Xi – выпуск (ВВ) i-ой отрасли,
Хj - выпуск (ВВ) j-ой отрасли,
аij – коэффициенты прямых затрат продукции i-ой отрасли на производство единицы продукции j-ой отрасли (аij = xij : Хj),
Yi – конечный спрос i-ой отрасли (вклад i-ой отрасли в ВВП).
1) Построим систему из двух уравнений, где Х1 и Х2 – неизвестные:
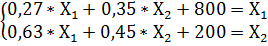 (1)
(1)
Преобразуем систему уравнений (1) в более удобную форму:
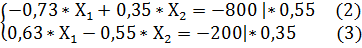
Умножаем обе части (2) уравнения на 0,55, а (3) уравнения на 0,35. Получаем такую модификацию системы уравнений (1):
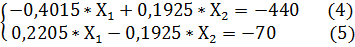
При суммировании уравнений (4) и (5) получаем следующее уравнение:
- 0,181 ∙ Х1 = - 510
Тогда:
Х1 = 2817,68
Х2 = (0,4015 ∙ 2817,68 – 440 ) / 0,1925 = 3591,16
Таким образом, суммарный продукт по экономике в целом будет равен:
Х1 + Х2 = 2817,68 + 3591,16 = 6408,84
ВВП (по условию задания, Y1 + Y2 = 800 + 200 = 1 000) составит 15,6% валового выпуска:
1 000 ∙ 100% / 6 408,84 = 15,6%
Промежуточное потребление определяется разницей между суммарным продуктом и ВВП и равно:
ПП = ВВ – ВВП = 6 408,84 – 1 000 = 5 408,84.
Промежуточное потребление больше ВВП в 5,409 раз (5 408,84 / 1 000).
2) Построим систему из двух уравнений, если прямые затраты первой продукции на производство единицы второй продукции уменьшатся на 20%: с 0,35 до 0,8*0,35.
То есть:
а12 = 0,28
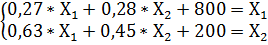 (6)
(6)
Преобразуем систему уравнений (6) в более удобную форму:
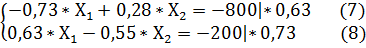
Умножаем обе части уравнения (7) на 0,63, а уравнения (8) на 0,73.
Получаем такую модификацию системы уравнений (6):
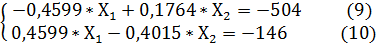
При суммировании уравнений (9) и (10) получаем следующее уравнение:
- 0,2251 ∙ Х2 = - 650
Откуда:
Х2 = 2 887,6
Х1 = (0,4015 ∙ 2 887,6 – 146 ) / 0,4599 = 2 203,46
Рассчитаем валовой выпуск по экономике в целом:
Х1 + Х2 = 2 887,6 + 2 203,46 = 5 091,06
Тогда промежуточное потребление определяется как разница между валовым выпуском и ВВП (который по условию задания равен Y1 + Y2 = 800 + 200 = 1000):
ПП = ВВ – ВВП = 5 091,06 – 1000 = 4091,06
Найдём показатель затратоёмкости ВВП до изменений. Он будет равен соотношению промежуточного потребления и ВВП:
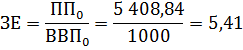
После уменьшения прямых затрат первой продукции на производство единицы второй продукции на 20% показатель затратоёмкости ВВП стал равен:
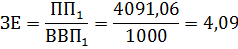
Экономическая эффективность производства повысилась.
Смотри ещё
- Основные макроэкономические показатели / Задача №19. Расчёт ВВП, ВНП, ЧВП, ЧНП, НД, ЛД, РЛД и др.
- Основные макроэкономические показатели / Задача №20. Расчёт реального ВВП, темпа прироста ВВП и темпа инфляции
- Основные макроэкономические показатели / Задача №21. Расчёт индекса-дефлятора ВВП
- Основные макроэкономические показатели / Задача №25. Расчёт чистого экспорта
- Основные макроэкономические показатели / Задача №26. Расчёт ВВП по доходам
- Основные макроэкономические показатели / Задача №27. Расчёт темпов прироста номинального ВВП, реального ВВП и дефлятора ВВП
- Основные макроэкономические показатели / Задача №62. Расчёт инвестиций
- Основные макроэкономические показатели / Задача №63. Расчёт частных сбережений
- Основные макроэкономические показатели / Задача №84. Расчёт темпа прироста реального ВВП
- Провалы рынка и государственное регулирование / Задача №195. Определение Парето-оптимального объема производства общественного блага
- Рынки факторов производства / Задача №187. Расчёт уровня занятости монополиса-монопсониста
- Система национальных счетов / Задача №1. Расчёт ВВП тремя методами
- Система национальных счетов / Задача №2. Расчёт ВВП, ВНД, ВС, ВРД и ЧК/ЧЗ
- Система национальных счетов / Задача №4. Расчёт ВДС, ВВП (тремя методами), ВП, ЧП, ВНД, ЧНД
- Система национальных счетов / Задача №5. Расчёт ВВП тремя методами, валовой прибыли, ВНД, ВНРД, НС, ЧК/ЧЗ
- Система национальных счетов / Задача №6. Построение счёта производства
- Система национальных счетов / Задача №7. Построение счёта производства и счёта образования доходов
- Система национальных счетов / Задача №8. Расчёт валовой прибыли экономики, построение счёта образования доходов
- Система национальных счетов / Задача №13. Расчёт валового выпуска на основе уравнения математической модели МОБ
- Система национальных счетов / Задача №14. Расчёт валового выпуска на основе уравнения математической модели МОБ
- Система национальных счетов / Задача №17. Расчёт валового выпуска, промежуточного потребления и ВВП на основе уравнения математической модели МОБ
- Система национальных счетов / Задача №18. Расчёт валовой добавленной стоимости сектора "Государственные учреждения"
- Спрос и предложение / Задача №4. Функция суммарного спроса
- Спрос и предложение / Задача №5. Функция суммарного спроса
- Спрос и предложение / Задача №35. Расчёт изменения величины спроса на картофель
- Спрос и предложение / Задача №44. Расчёт объёма неудовлетворённого спроса
- Спрос и предложение / Задача №48. Расчёт излишков и общей суммы дотации
- Спрос и предложение / Задача №128. Расчёт параметров равновесия и величины дефицита
- Спрос и предложение / Задача №138. Расчёт параметров равновесия
- Спрос и предложение / Задача №169. Нахождение уравнений кривых спроса и предложения























