Оптимальный выпуск фирмы

В отрасли совершенной конкуренции установилась цена:

Р = 50

Средние переменные затраты конкурентной фирмы выражены формулой:

AVC = 50 + (Q – 30)²

Фиксированные затраты равны 10 000.

Найти оптимальный выпуск фирмы.

Решение

Функция общих затрат монополии имеет вид

ТС = 200 + 30Q,

функция спроса на её продукцию

Р = 60 - 0,2Q.

Определить цену, при которой фирма максимизирует прибыль.

Решение

Найти максимум прибыли монополиста, если известно, что спрос на его продукцию описывается функцией:

Q = 165 - 0,5 × P

и функция общих затрат равна:

TC = 5500 + 30 × Q + Q²

Решение

Даны функция спроса на продукцию монополиста

Q = 25 - P

и функция средних переменных затрат

AVC = 4 + 0,5 × Q.

Известно, что максимум прибыли монополиста равен 23,5. Найти его фиксированные затраты.

Решение

Допустим, общие затраты монополии равны

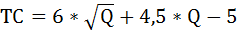
при спросе на её продукцию

Q = 32 – 4 × Р.

Найти оптимальную цену и выпуск продукции, обеспечивающие наибольшую прибыль. Вычислить эту прибыль.

Решение

Даны функция спроса на продукцию монополиста

Q = 25 - P

и функция общих затрат

TC = 50 + 4 × Q + 0,5 × Q².

Сколько теряет монополист, если правительственные органы ограничат цену на его продукцию уровнем 15 денежных единиц.

Решение

Монополия максимизирует выручку при целевой прибыли не ниже 1500 единиц. Известны функция спроса

P = 304 - 2 × Q

и функция затрат

ТС = 500 + 4 × Q + 8 × Q²

а) Определить оптимальный объём выпуска и цену.

б) Какими были бы оптимальный выпуск и цена, если бы монополия преследовала цель максимизации прибыли?

Решение

У монополистически конкурентной фирмы известна функция цены:

P = 1000 – 10 × Q

и функция совокупных издержек:

TC = 100 + 5 × Q.

1. Определите оптимальный объём выпуска и цену товара у этой фирмы. Чему равна её экономическая прибыль?

2. Если бы данный сегмент рынка был совершенно конкурентным, то сколько продукции производилось бы и по какой цене она бы продавалась?

Решение

Функция общих издержек совершенно конкурентной фирмы

TC = 150 – 18Q + Q².

В точке оптимального выпуска фирма получает прибыль в размере 250 ед.

Определите значение рыночной цены продукции. Каков ее оптимальный объем выпуска?

Решение

Монополия стремится максимизировать выручку, но при этом ее акционеры не готовы допустить снижения уровня прибыли ниже 2000. Известны функции спроса и затрат:

Р = 400 – 2 × Q,

ТС = 400 + 8 × Q + 2 × Q².

Определите:

а) оптимальный объем выпуска и цену;
b) каким был бы оптимальный выпуск и цена, если бы монополия
преследовала цель максимизации выручки без ограничений на значение прибыли.

Решение