Задача №47. Построение модели линейной регрессии
Имеются данные о количестве проданного товара и его цене:
| Количество (тыс. / день) | Цена (руб. / за ед.) |
|---|---|
| 8 | 5,0 |
| 10 | 3,5 |
| 24 | 2,0 |
| 16 | 2,5 |
Изобразить данные на графике, построить модель линейной регрессии, определить тесноту связи. Объяснить значение коэффициентов.
Решение:
Изобразим данные на графике:
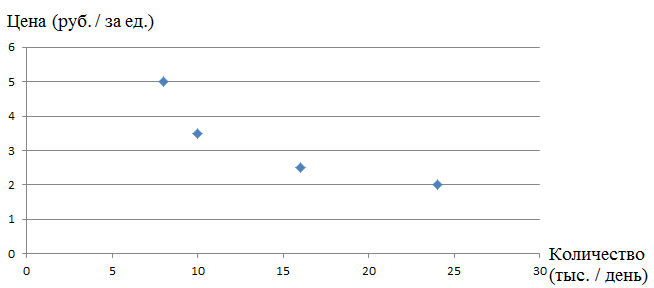
Для расчёта параметров уравнения линейной регрессии:
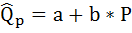
(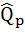 – количество проданного товара, зависящее от цены Р),
– количество проданного товара, зависящее от цены Р),
необходимо решить систему нормальных уравнений относительно a и b:
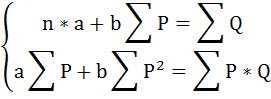
Построим таблицу исходных и расчётных данных.
Таблица 1 Расчетные данные для оценки линейной регрессии
| № п/п | Р | Q | P2 | Q2 | P×Q | 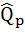 |
|---|---|---|---|---|---|---|
| 1 | 5 | 8 | 25 | 64 | 40 | 6 |
| 2 | 3,5 | 10 | 12,25 | 100 | 35 | 13,28571 |
| 3 | 2 | 24 | 4 | 576 | 48 | 20,57143 |
| 4 | 2 | 16 | 6,25 | 256 | 40 | 18,14286 |
| Итого | 13 | 58 | 47,5 | 996 | 163 | 58 |
| Среднее | 3,25 | 14,5 | х | х | 40,75 | х |
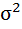 |
1,3125 | х | х | х | х | х |
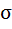 |
1,145644 | х | х | х | х | х |
Средние значения P и Q определим по формуле средней арифметической простой:
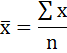
Среднее квадратическое отклонение рассчитаем по формуле:
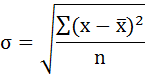
Возведя в квадрат полученное значение, получим дисперсию:
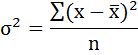
Параметры уравнения можно определить также и по формулам:
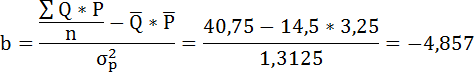
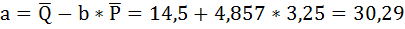
Таким образом, уравнение регрессии имеет вид:
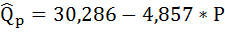
Подставим в данное уравнение исходные значения Р и найдём сумму расчётных значений Q (последняя графа таблицы).
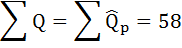
Так как суммы исходных и расчётных значений Q совпадают, следовательно, параметры уравнения найдены верно.
С увеличением цены на 1 руб. количество проданного товара снизится в среднем на 4,86 тыс.
Найдём коэффициент корреляции для оценки силы связи между двумя переменными – количеством проданного товара (Q) и ценой (P):
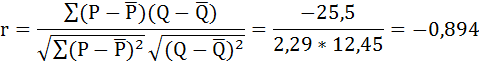
Расчётная таблица:
| № п/п | P | Q | 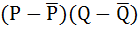 |
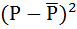 |
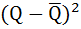 |
|---|---|---|---|---|---|
| 1 | 5 | 8 | -11,375 | 3,0625 | 42,25 |
| 2 | 3,5 | 10 | -1,125 | 0,0625 | 20,25 |
| 3 | 2 | 24 | -11,875 | 1,5625 | 90,25 |
| 4 | 2,5 | 16 | -1,125 | 0,5625 | 2,25 |
| Итого | 13 | 58 | -25,5 | 5,25 | 155 |
| Среднее | 3,25 | 14,5 | - | 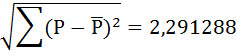 |
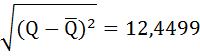 |
Оценим корреляцию по шкале Чеддока.
| Коэффициент корреляции по абсолютной величине | Интерпретация |
|---|---|
| до 0,3 | слабая |
| 0,3 - 0,5 | умеренная |
| 0,5 - 0,7 | заметная |
| 0,7 - 0,9 | высокая |
| 0,9 - 1,0 | весьма высокая |
Полученный коэффициент корреляции указывает на высокую связь между ценой и количеством проданного товара. Знак минус показывает обратную зависимость между ценой и объёмом продаж.
Смотри ещё
- Выборочное наблюдение / Задача №39. Расчёт предела, в котором находятся средние затраты времени
- Средние величины и показатели вариации / Задача №3. Расчёт среднего времени
- Средние величины и показатели вариации / Задача №5. Расчёт средней арифметической взвешенной в интервальном ряду распределения
- Средние величины и показатели вариации / Задача №6. Расчёт показателей вариации
- Средние величины и показатели вариации / Задача №7. Расчёт коэффициента вариации
- Средние величины и показатели вариации / Задача №9. Расчёт среднего квадрата индивидуальных значений признака
- Средние величины и показатели вариации / Задача №10. Расчёт среднего квадрата отклонений вариантов признака от произвольной величины
- Средние величины и показатели вариации / Задача №12. Расчёт коэффициента вариации
- Средние величины и показатели вариации / Задача №13. Расчёт среднего квадрата отклонений индивидуальных значений признака от произвольной величины
- Средние величины и показатели вариации / Задача №22. Виды дисперсии и их расчёт
- Средние величины и показатели вариации / Задача №23. Расчёт показателей асимметрии и эксцесса
- Средние величины и показатели вариации / Задача №24. Расчёт показателей вариации по несгруппированным данным
- Средние величины и показатели вариации / Задача №26. Расчёт среднего удоя
- Средние величины и показатели вариации / Задача №29. Расчёт крайних значений вариационного ряда
- Средние величины и показатели вариации / Задача №30. Расчёт коэффициента вариации
- Средние величины и показатели вариации / Задача №43. Расчёт описательных статистик
- Средние величины и показатели вариации / Задача №45. Расчёт абсолютных и относительных показателей вариации
- Средние величины и показатели вариации / Задача №48. Расчёт показателей вариации
- Статистика населения / Задача №2. Расчёт средней численности населения
- Статистика населения / Задача №11. Расчёт коэффициентов брачности и разводимости
- Статистические методы изучения взаимосвязей / Задача №53. Расчёт точечного прогноза
- Статистические методы изучения взаимосвязей / Задача №54. Расчёт коэффициента корреляции
- Эконометрика / Задача №1 Построение уравнения регрессии
- Эконометрика / Задача №3. Расчёт параметров регрессии и корреляции с помощью Excel
- Эконометрика / Задача №4. Построение регрессионной модели с использованием фиктивной переменной























