Функция полезности
Задача №63. Расчёт цен товаров Х и Y
Функция общей полезности индивида от потребления блага X имеет вид:
TUx = 40X – X2
а от потребления блага Y:
TUy = 18Y – 4Y2
Он потребляет 10 единиц блага X и 2 единицы блага Y. Предельная полезность денег составляет 1/2.
Определите цены товаров X и Y.
Задача №64. Расчёт оптимального объёма потребления
У Оксаны есть 30 рублей. Она хочет купить шоколадки «Шок» ценой 3 р. Полезность от этой покупки она оценивает функцией:
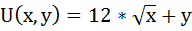
х – приобретённое количество шоколадок,
y – оставшаяся часть дохода.
Сколько купит шоколадок «Шок» рациональная Оксана?
Задача №65. Определение рационального выбора потребителя
Потребитель имеет функцию полезности:
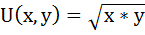
и может на свой доход равный 100 единицам приобретать только эти два товара по ценам:
Px = 2
Py = 5
Определить рациональный выбор потребителя. Какой максимальный уровень полезности достижим?
Задача №66. Расчёт оптимального объёма потребления
Определите оптимальный для потребителя объем блага Q, если известно, что функция полезности индивида от обладания этим благом имеет вид:
1) U(Q) = 1 – 2Q2;
2) U(Q) = 5 + Q – Q2;
3) U(Q) = Q2 – Q3.
Как будут выглядеть функции предельной полезности?
Задача №67. Расчёт предельной полезности
Определите предельную полезность благ х и у, если функция полезности имеет вид:
1) U(x;y) = 2х + у;
2) U(x;y) = 2х2 + у;
3) U(x;y) = хβу1-β
Задача №68. Расчёт оптимального набора потребителя
Потребитель свой располагаемый доход в размере 90 руб. тратит на приобретение кефира и картофеля.
Стоимость продуктов питания:
Ркеф = 15 руб. за 1 л.
Ркар= 3 руб. за 1 кг.
Предпочтения потребителя описываются следующей функцией полезности:
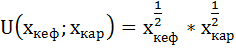
Насколько изменится оптимальный набор потребителя, если его предпочтения станут описываться функцией полезности вида:
1) 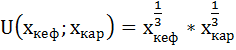
2) 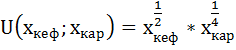
Задача №69. Расчёт оптимального объёма потребления
Маша тратит 140 р. в месяц на персики и клубнику.
а) Общая полезность персиков независимо от количества клубники оценивается в:
TU(x) = 30x – 2x2,
где
х – количество килограммов персиков в месяц.
Общая полезность клубники также не зависит от наличия персиков и составляет:
TU(y) = 20y – y2,
где
у – количество килограммов клубники.
Цена персиков – 10 р. за килограмм, а клубники – 20 р.
Сколько купит клубники рациональная Маша?
б) Предположим, что изменились условия в том, что касается полезности клубники:
TU(y) = 20y – ху.
в) Что будет, если общая полезность задаётся формулой:
TU(x,y) = 20y*30x – xy ?
Задача №173. Расчёт отимального объёма потребления
Определите оптимальный для потребителя объем блага Q, если известно, что функция полезности индивида от обладания этим благом имеет вид:
1) U(Q)= 1 – 5 × Q2
2) U(Q)= 5 + Q – Q2
3) U(Q) = Q2 – 5 × Q3
Как будут выглядеть функции предельной полезности? Проиллюстрируйте ответ.























