Задача №67. Расчёт предельной полезности

Поведение потребителя

Определите предельную полезность благ х и у, если функция полезности имеет вид:

1) U(x;y) = 2х + у;

2) U(x;y) = 2х²+ у;

3) U(x;y) = х^βу^1-β

Решение:

Предельную полезность блага х найдём как частную производную функции общей полезности по аргументу х:

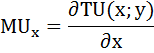
Формула предельной полезности х

1) MU_x = (2х + у)’ = 2;

2) MU_x= (2х² + у)’ = 4x;

3) MU_x= (х^βу^1-β)’ = βх^β-1у^1-β= β(х/у)^β-1

Аналогично найдём предельную полезность блага у, как частную производную функции общей полезности по аргументу у:

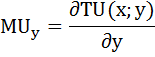
Формула предельной полезности у

1) MU_у= (2х + у)’ = 1;

2) MU_у= (2х²+ у)’ = 1;

3) MU_у= (х^βу^1-β)’ = (1 – β)х^βу^-β= (1 – β) × (х/у)^β

Функция полезности Предельная полезность Полезность

Совершенная конкуренция

Определение рыночной цены Решение

Темп роста

Расчёт относительных показателей динамики Решение

Средняя арифметическая

Расчёт средней цены Решение

Расчёт годовой инфляции по квартальным данным Решение

Расчёт амортизационных отчислений, бухгалтерской и экономической прибыли Решение

Издержки

Расчёт бухгалтерской и экономической прибыли и ставки налога на прибыль Решение

Расчёт экономической и бухгалтерской прибыли Решение

Расчёт амортизационных отчислений Решение

Экономическая прибыль

Расчёт бухгалтерской и экономической прибыли Решение

Расчёт бухгалтерской и экономической прибыли Решение

Есть график!

Расчёт налогового бремени покупателя и продавца и чистых общественных потерь

Счёт операций с капиталом

Составление счёта операций с капиталом подробнее

Смотри ещё

ВНД, ВРП, ВНС

Построение счёта операций с капиталом подробнее

Счёт использования располагаемого дохода

Построение счёта использования располагаемого дохода подробнее

Счёт производства

Построение счёта производства подробнее

Составление плана погашения кредита подробнее

Расчёт параметров регрессии и корреляции с помощью Excel Решение

Расчёт ставки налога Решение

Расчёт размера потоварной дотации Решение

Рыночное рановесие

Расчёт излишков и общей суммы дотации подробнее

Рыночное равновесие

Расчёт суммы налога, излишков и чистых потерь Решение

Рыночное равновесие

Расчёт налогового бремени, размера потерь «мёртвого груза» Решение

Эластичность

Расчёт изменения величины спроса на картофель Решение

Расчёт добавленной стоимости Решение