Задача №66. Расчёт оптимального объёма потребления

Определите оптимальный для потребителя объем блага Q, если известно, что функция полезности индивида от обладания этим благом имеет вид:

1) U(Q) = 1 – 2Q²;

2) U(Q) = 5 + Q – Q²;

3) U(Q) = Q² – Q³.

Как будут выглядеть функции предельной полезности?

Решение:

Функции предельной полезности определим с помощью первой производной от функции общей полезности.

1) MU(Q) = (1 – 2Q²)’ = – 4Q

2) MU(Q) = (5 + Q – Q²)’ = 1 – 2Q

3) MU(Q) = (Q² – Q³)’ = 2Q – 3Q²

Общая полезность (TU) достигает своего максимума, когда предельная полезность (MU) равна нулю:

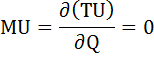
Таким образом, оптимальный для потребителя объем:

1) MU(Q)= – 4Q = 0, Q = 0

Изобразим функции общей и предельной полезности графически:

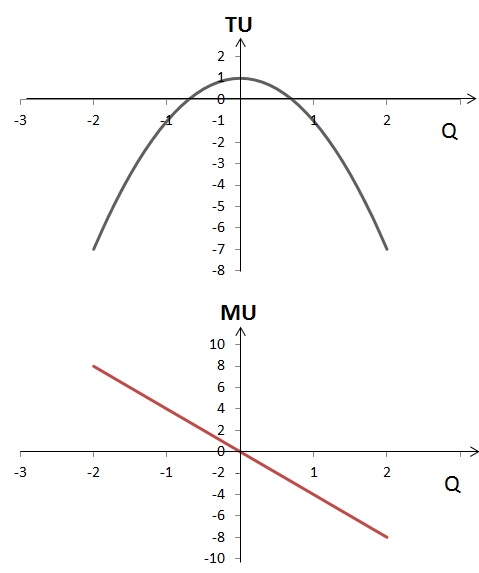
Как видно из графика, оптимальный для потребителя объем блага Q = 0. Общая полезность в этой точке максимальна.

2) MU(Q) = 1 – 2Q = 0, Q = 1/2

Графически функции общей и предельной полезности для данного случая будут выглядеть следующим образом:

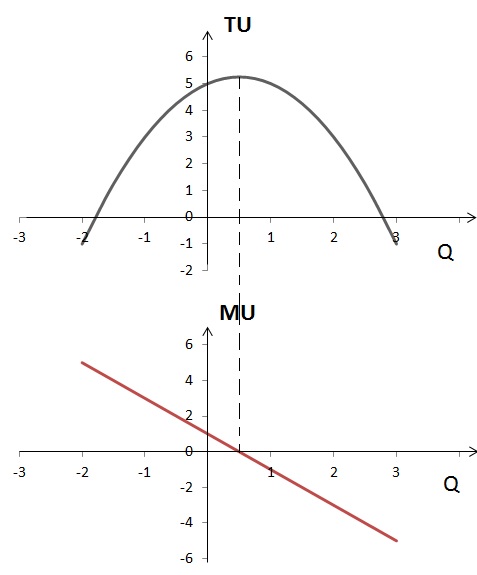
Как видно из графика, общая полезность максимальна при потреблении 1/2 единицы блага Q.

Внимательный читатель может возразить, что совсем необязательно было строить графики TU и MU с отрицательными значениями Q, так как значения функции при Q < 0 экономического смысла не имеют. Однако? как мы увидим далее, это окажется для нас полезным.

3) MU(Q) = 2Q – 3Q²

Приравнивая к нулю производную функции общей полезности получим квадратное уравнение:

2Q – 3Q² = 0,

Корни этого уравнения:

Q = 0 и Q = 2/3.

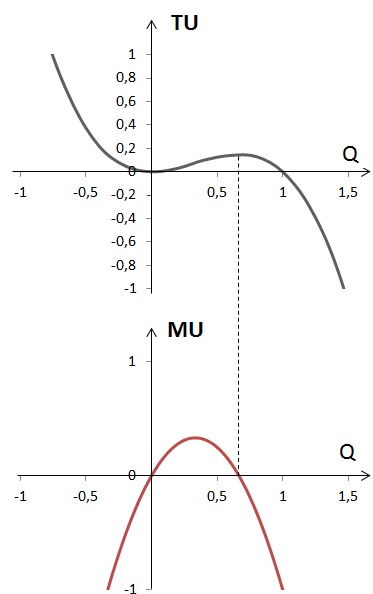
Как видно из графика, максимум функции общей полезности находится лишь в точке Q = 2/3, который и будет оптимальным для потребителя.