Задача №14. Расчёт валового выпуска на основе уравнения математической модели МОБ
Условно примем, что экономика состоит из двух секторов. Коэффициенты прямых затрат соответствуют размерности матрицы 2x2. Конечный спрос по каждому сектору составляет, соответственно Yi.
| Коэффициенты прямых затрат, aij | Конечный спрос,Yi | |
|---|---|---|
| а11=0,35 | а12=0,55 | Y1=2600 |
| а21=0,25 | а22=0,35 | Y2=2400 |
Определите:
1) валовой выпуск по экономике в целом (Х1 + Х2) и соотношение валового выпуска и ВВП, а также ВВП и промежуточного потребления;
2) насколько (в %) возрастёт валовой выпуск в целом по экономике, если увеличатся прямые затраты на единицу продукции: по а21 с 0,25 до 0,30 и по а22 с 0,35 до 0,40.
Примечание: Для расчетов необходимо построить два уравнения: уравнение по первой строке и уравнение по второй строке балансовой таблицы, используя уравнение математической модели межотраслевого баланса. Вопросы различий в оценке выпуска (валового выпуска) и ВВП здесь не рассматриваются.
Решение:
Уравнение математической модели межотраслевого баланса в общем виде имеет вид:
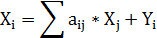
где
Xi – выпуск (ВВ) i-ой отрасли,
Хj - выпуск (ВВ) j-ой отрасли,
аij – коэффициенты прямых затрат продукции i-ой отрасли на производство единицы продукции j-ой отрасли (аij = xij : Хj),
Yi – конечный спрос i-ой отрасли (вклад i-ой отрасли в ВВП).
1) Построим систему из двух уравнений, где Х1 и Х2 – неизвестные:
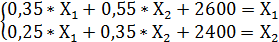 (1)
(1)
Преобразуем систему уравнений (1) в более удобную форму:
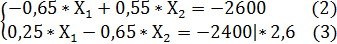
Умножаем обе части уравнения (3) на 2,6. Получаем такую модификацию системы уравнений (1):
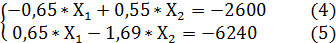
При суммировании уравнений (4) и (5) получаем следующее уравнение:
- 1,14 ∙ Х2 = - 8 840
Тогда:
Х2 = 7 754,39
Х1 = (1,69 ∙ 7 754,39 – 6 240 ) / 0,65 = 10 561,4
Таким образом, суммарный продукт по экономике в целом равен:
Х1 + Х2 = 7 754,39 + 10 561,4 = 18 315,79
ВВП (по условию задания, Y1 + Y2 = 2 600 + 2 400 = 5 000) составит 27,3% валового выпуска (5 000 / 18 315,79 ∙ 100%).
Промежуточное потребление определяется разницей между суммарным продуктом и ВВП и равно:
13 315,79 (18 315,79 – 5 000).
Промежуточное потребление больше ВВП в 2,66 раза (13 315,79 / 5 000).
2) Построим систему из двух уравнений, если прямые затраты на единицу продукции возрастут: по а21 с 0,25 до 0,30 и по а22 с 0,35 до 0,40.
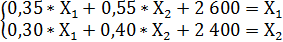 (6)
(6)
Преобразуем систему уравнений (6) в более удобную форму:
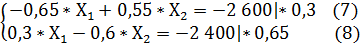
Умножаем обе части уравнения (7) на 0,3, а уравнение (8) на 0,65.
Получаем такую модификацию системы уравнений (6):
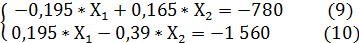
При суммировании уравнений (9) и (10) получаем следующее уравнение:
- 0,225 ∙ Х2 = - 2 340
Откуда:
Х2 = 10 400
Х1 = (0,39 ∙ 10 400 – 1 560 ) / 0,195 = 12 800
Рассчитаем валовой выпуск по экономике в целом:
Х1 + Х2 = 10 400 + 12 800 = 23 200
Следовательно, валовой выпуск возрастёт на 26,7%:
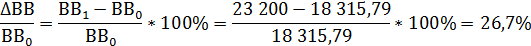
Смотри ещё
- Основные макроэкономические показатели / Задача №2. Расчёт номинального и реального ВВП, индексов Пааше, Ласпейреса и Фишера
- Основные макроэкономические показатели / Задача №16. Расчёт ВВП (двумя способами), ВНП, ЧНП, НД, ЛД, РЛД и др
- Основные макроэкономические показатели / Задача №17. Расчёт стоимости конечной и промежуточной продукции, ВВП и добавленной стоимости
- Основные макроэкономические показатели / Задача №19. Расчёт ВВП, ВНП, ЧВП, ЧНП, НД, ЛД, РЛД и др.
- Основные макроэкономические показатели / Задача №20. Расчёт реального ВВП, темпа прироста ВВП и темпа инфляции
- Основные макроэкономические показатели / Задача №21. Расчёт индекса-дефлятора ВВП
- Основные макроэкономические показатели / Задача №25. Расчёт чистого экспорта
- Основные макроэкономические показатели / Задача №26. Расчёт ВВП по доходам
- Основные макроэкономические показатели / Задача №27. Расчёт темпов прироста номинального ВВП, реального ВВП и дефлятора ВВП
- Основные макроэкономические показатели / Задача №62. Расчёт инвестиций
- Основные макроэкономические показатели / Задача №63. Расчёт частных сбережений
- Основные макроэкономические показатели / Задача №84. Расчёт темпа прироста реального ВВП
- Провалы рынка и государственное регулирование / Задача №195. Определение Парето-оптимального объема производства общественного блага
- Рынки факторов производства / Задача №187. Расчёт уровня занятости монополиса-монопсониста
- Система национальных счетов / Задача №1. Расчёт ВВП тремя методами
- Система национальных счетов / Задача №2. Расчёт ВВП, ВНД, ВС, ВРД и ЧК/ЧЗ
- Система национальных счетов / Задача №4. Расчёт ВДС, ВВП (тремя методами), ВП, ЧП, ВНД, ЧНД
- Система национальных счетов / Задача №5. Расчёт ВВП тремя методами, валовой прибыли, ВНД, ВНРД, НС, ЧК/ЧЗ
- Система национальных счетов / Задача №6. Построение счёта производства
- Система национальных счетов / Задача №7. Построение счёта производства и счёта образования доходов
- Система национальных счетов / Задача №8. Расчёт валовой прибыли экономики, построение счёта образования доходов
- Система национальных счетов / Задача №13. Расчёт валового выпуска на основе уравнения математической модели МОБ
- Система национальных счетов / Задача №15. Расчёт валового выпуска на основе уравнения математической модели МОБ
- Система национальных счетов / Задача №17. Расчёт валового выпуска, промежуточного потребления и ВВП на основе уравнения математической модели МОБ
- Система национальных счетов / Задача №18. Расчёт валовой добавленной стоимости сектора "Государственные учреждения"
- Спрос и предложение / Задача №35. Расчёт изменения величины спроса на картофель
- Спрос и предложение / Задача №182. Расчёт коэффициента эластичности спроса и валовой выручки
- Фискальная политика / Задача №36. Расчёт потенциального ВВП
- Фискальная политика / Задача №38. Определение правительственной политики для стабилизации экономики
- Фискальная политика / Задача №39. Выбор правительственной политики для стабилизации экономики























