Задача №84. Расчёт оптимального объёма потребления
Студент приобретает кофе и пирожки. Цена чашки кофе $2, пирожка $3. При этом он располагает бюджетом в размере $23. Известны предпочтения студента в виде общей полезности:
| Количество | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| TU кофе, ютилей | 20 | 36 | 50 | 62 | 72 | 80 | 86 |
| TU пирожков, ютилей | 36 | 66 | 93 | 117 | 135 | 144 | 150 |
Как потратить максимум бюджета так, чтобы купить набор этих двух благ с наибольшей полезностью? Сколько она составит?
Решение:
Оптимальный объём потребления достигается при выполнении второго закона Госсена – закона равной маржинальной (предельной) полезности на единицу затрат: отношение предельной полезности блага к его цене должно быть одинаковым для всех благ.
Запишем этот закон в виде тождества:
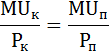
где
MUк – предельная полезность кофе,
MUп – предельная полезность пирожков,
Pк – цена кофе,
Pп – цена пирожков.
Перепишем это равенство в более удобном виде:
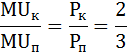
Значит, цены на кофе и пирожки относятся как 2:3. Теперь надо найти такую комбинацию предельных полезностей, чтобы они относились также как 2:3.
Рассчёт предельной полезности произведём по формуле:
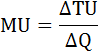
где
ΔTU – приращение общей полезности (TU1 – TU0),
ΔQ – приращение количества (Q1 – Q0).
Так как количество в нашей задаче прирастает каждый раз на единицу ΔQ = 1, можно упростить эту формулу так:
MU = ΔTU
| Количество | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| TU кофе, ютилей | 20 | 36 | 50 | 62 | 72 | 80 | 86 |
| MU кофе, ютилей | 20 | 16 | 14 | 12 | 10 | 8 | 6 |
| TU пирожков, ютилей | 36 | 66 | 93 | 117 | 135 | 144 | 150 |
| MU пирожков, ютилей | 36 | 30 | 27 | 24 | 18 | 9 | 6 |
В данной задаче три варианта соотношений 2:3 предельных полезностей:
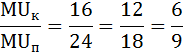
Выпишем эти наборы двух благ:
2 чашки кофе и 4 пирожка, или 4 кофе и 5 пирожков, или 7 кофе и 6 пирожков.
Так как бюджет в $23 должен быть израсходован максимально, выберем из этих комбинаций оптимальную.
Подставим эти значения в формулу бюджетного ограничения:
I = Pк*Qк + Pп*Qп
где
I – бюджет или доход потребителя,
Pк, Pп – цены на кофе и пирожки,
Qк, Qп – объём потребления кофе и пирожков соответственно.
При Qк = 2, Qп = 4 бюджетное ограничение имеет вид:
23 > 2 × 2 + 3 × 4.
В этом случае бюджет израсходован не полностью.
При Qк = 4, Qп = 5 бюджетное ограничение имеет вид:
23 = 2*4 + 3*5.
Получили верное тождество. Следовательно, оптимальный объем потребления кофе – 4 чашки, а пирожков – 5 штук. При этом бюджет истрачен полностью.
Общая полезность составит:
TU = 62 + 135 = 197.

Рыночное равновесие
Смотри ещё
- Поведение потребителя / Задача №58. Расчёт дохода потребителя
- Поведение потребителя / Задача №59. Расчёт общей и предельной полезности
- Поведение потребителя / Задача №60. Расчёт общей полезности
- Поведение потребителя / Задача №61. Расчёт оптимального объёма потребления двух благ
- Поведение потребителя / Задача №62. Расчёт цен товаров Х и Y
- Поведение потребителя / Задача №63. Расчёт цен товаров Х и Y
- Поведение потребителя / Задача №64. Расчёт оптимального объёма потребления
- Поведение потребителя / Задача №65. Определение рационального выбора потребителя
- Поведение потребителя / Задача №66. Расчёт оптимального объёма потребления
- Поведение потребителя / Задача №67. Расчёт предельной полезности
- Поведение потребителя / Задача №68. Расчёт оптимального набора потребителя
- Поведение потребителя / Задача №69. Расчёт оптимального объёма потребления
- Поведение потребителя / Задача №70. Расчёт цен товаров X и Y
- Поведение потребителя / Задача №145. Расчёт потоварного и аккордного налога
- Поведение потребителя / Задача №173. Расчёт отимального объёма потребления
- Поведение потребителя / Задача №201. Расчёт оптимального объёма потребления






















