Затраты страница 4
Задача №123. Расчёт фиксированных затрат
Известна функция спроса на продукцию монополиста
Q = 220 - 4 × P,
и дана функция предельных затрат
MC = 10 + 4 × Q.
Известно, что максимум прибыли монополиста равен 125. Найти его фиксированные затраты.
Задача №124. Расчёт монопольной цены
По данным исследования рынка, кривая спроса представляет собой отрезок прямой, а величина спроса при цене, равной 5 р. за штуку, составляет 300 тыс. штук в год и падает на 30 тыс. штук при увеличении цены на каждый рубль. Какую цену выгодно установить монополисту, если постоянные издержки составляют 150 тыс. р. в год, переменные затраты на единицу товара равны 3 р.?
Задача №127. Расчёт прибыли, оптимальной цены и выпуска продукции
Допустим, общие затраты монополии равны
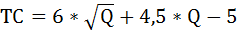
при спросе на её продукцию
Q = 32 – 4 × Р.
Найти оптимальную цену и выпуск продукции, обеспечивающие наибольшую прибыль. Вычислить эту прибыль.

Совершенная конкуренция
Задача №132. Расчёт максимального числа дней ремонта
Иванов хочет отремонтировать квартиру. Он может нанять мастеров и заплатить им 15 тыс. р., а может все сделать сам, тогда ремонт будет стоить ему только 5 тыс. р. (цена материалов). Но придется взять отпуск без сохранения заработка. В день он зарабатывает 500 р. Какое максимальное число дней может потратить на ремонт Иванов, чтобы не нести убытки.
Задача №135. Расчёт потерь монополиста в результате государственного вмешательства
Даны функция спроса на продукцию монополиста
Q = 25 - P
и функция общих затрат
TC = 50 + 4 × Q + 0,5 × Q2.
Сколько теряет монополист, если правительственные органы ограничат цену на его продукцию уровнем 15 денежных единиц.
Задача №186. Расчёт издержек фирмы
Информация о деятельности фирмы, кроме представленной в таблице, оказалась утраченной. Восстановите недостающую информацию об издержках фирмы.
| Q | TC | VC | FC | AC | AVC | AFC | MC |
|---|---|---|---|---|---|---|---|
| 1 | 30 | ||||||
| 2 | 18 | ||||||
| 3 | 15 | ||||||
| 4 | 7 | ||||||
| 5 | 4 | 2 | |||||
| 3,5 | 1 |

Экономическая прибыль





















