Спрос
Задача №4. Функция суммарного спроса
а) Определить функцию суммарного спроса на основании данных об индивидуальном спросе:
Q(1) = 100 – 5 P при P≤ 20 и 0 при Р > 20,
Q(2) = 50 – 8 P при P≤ 10 и 0 при Р > 10,
Q(3) = 56 – 4 P при P≤ 14 и 0 при Р > 14.
б) Найти эластичность спроса в точке P = 12.
Задача №5. Функция суммарного спроса
Известны данные об индивидуальном спросе:
Q(1) = 80 – 8 P при P ≤ 10 и 0 при Р > 10,
Q(2) = 50 – 10 P при P ≤ 5 и 0 при Р > 5,
Q(3) = 32 – 4 P при P ≤ 8 и 0 при Р > 8.
а) Выведите уравнение кривой спроса аналитически.
б) Получите формулу эластичности по абсолютной величине в зависимости от цены.
Задача №13. Расчёт валового выпуска на основе уравнения математической модели МОБ
Предположим, что экономика состоит из двух отраслей. Коэффициенты прямых затрат соответствуют размерности матрицы 2x2; конечный спрос по каждой из двух отраслей равен, соответственно Yi.
| Коэффициенты прямых затрат, aij | Конечный спрос,Yi | |
|---|---|---|
| а11=0,35 | а12=0,55 | Y1=2600 |
| а21=0,25 | а22=0,35 | Y2=2400 |
Определите:
1) валовой выпуск по экономике в целом (Х1 + Х2);
2) соотношение валового выпуска и ВВП, а также ВВП и промежуточного потребления;
3) насколько изменится валовой выпуск (%), если прямые затраты на единицу продукции сократятся: по а11 с 0,35 до 0,30 и по а12 с 0,55 до 0,50.
Примечание: Для расчетов необходимо построить два уравнения: уравнение по первой строке и уравнение по второй строке балансовой таблицы, используя уравнение математической модели межотраслевого баланса. Вопросы различий в оценке выпуска (валового выпуска) и ВВП здесь не рассматриваются.
Задача №14. Расчёт валового выпуска на основе уравнения математической модели МОБ
Условно примем, что экономика состоит из двух секторов. Коэффициенты прямых затрат соответствуют размерности матрицы 2x2. Конечный спрос по каждому сектору составляет, соответственно Yi.
| Коэффициенты прямых затрат, aij | Конечный спрос,Yi | |
|---|---|---|
| а11=0,35 | а12=0,55 | Y1=2600 |
| а21=0,25 | а22=0,35 | Y2=2400 |
Определите:
1) валовой выпуск по экономике в целом (Х1 + Х2) и соотношение валового выпуска и ВВП, а также ВВП и промежуточного потребления;
2) насколько (в %) возрастёт валовой выпуск в целом по экономике, если увеличатся прямые затраты на единицу продукции: по а21 с 0,25 до 0,30 и по а22 с 0,35 до 0,40.
Примечание: Для расчетов необходимо построить два уравнения: уравнение по первой строке и уравнение по второй строке балансовой таблицы, используя уравнение математической модели межотраслевого баланса. Вопросы различий в оценке выпуска (валового выпуска) и ВВП здесь не рассматриваются.
Задача №35. Расчёт изменения величины спроса на картофель
Спрос населения на картофель характеризуется следующими показателями эластичности: по цене (-0,6); по доходу 0,8.
В будущем году общий уровень цен не изменится, доход населения увеличится на 4% и цена картофеля возрастет на 5%.
Определите, на сколько изменится величина спроса на картофель.

Рыночное равновесие
Задача №44. Расчёт объёма неудовлетворённого спроса
Функция спроса населения на данный товар:
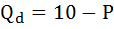
Функция предложения данного товара
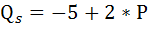
Предположим, на данный товар установлена фиксированная цена на уровне 3 ден. ед.
Определить объём неудовлетворённого спроса.
Задача №48. Расчёт излишков и общей суммы дотации
Функция спроса населения на данный товар имеет вид:
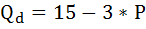
Функция предложения данного товара:
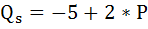
Предположим, что данный товар дотируется из бюджета в размере 2 ден. ед.
Определить:
а) излишек покупателя и излишек продавца до и после введения дотации;
б) общую сумму расходов бюджета на дотирование товара.
Задача №95. Определение рыночной цены
Сто фирм в условиях совершенной конкуренции имеют следующую зависимость общих издержек от объёма выпуска:
| Объём выпуска фирмы | 800 | 900 | 1000 | 1100 |
| Общие издержки фирмы, тыс. р. | 40 | 45,5 | 51,6 | 58,2 |
Шкала рыночного спроса показана в следующей таблице:
| Величина рыночного спроса | 80 000 | 90 000 | 100 000 | 110 000 |
| Цена, р. | 70 | 65 | 61 | 58 |
а) Определите рыночную цену.
б) Является ли производство прибыльным? Какую экономическую прибыль (убыток) получает одна фирма?
Задача №106. Определение количества фирм в отрасли
Известно, что рынок бензина в стране X находится в условиях совершенной конкуренции. Спрос на бензин описывается уравнением:
Qd = 200 - 20P
Средние издержки типичной бензоколонки равны:
АС = 5 + (Q - 5)2
Какое число бензоколонок должно действовать в отрасли в долгосрочной перспективе?
Задача №108. Расчёт цены и объёма производства, максимизирующих прибыль
Спрос на продукцию конкурентной отрасли:
Qd = 55 – P
Предложение:
Qs = 2P – 5
Если у одной из фирм отрасли восходящий участок кривой предельных издержек:
МС = 3Q + 5
При каких цене и объёме производства фирма максимизирует прибыль?






















