Предельные издержки страница 2
Задача №114. Определение прямой и обратной функции предложения
Функция общих затрат совершенно конкурентной фирмы имеет вид:
ТС = Q3 - 16Q2 + 100Q + 500.
Запишите уравнение прямой и обратной функции предложения данной фирмы в краткосрочном периоде.
Задача №115. Расчёт цены, при которой фирма максимизирует прибыль
Функция общих затрат монополии имеет вид
ТС = 200 + 30Q,
функция спроса на её продукцию
Р = 60 - 0,2Q.
Определить цену, при которой фирма максимизирует прибыль.
Задача №116. Расчёт максимума прибыли монополиста
Найти максимум прибыли монополиста, если известно, что спрос на его продукцию описывается функцией:
Q = 165 - 0,5 × P
и функция общих затрат равна:
TC = 5500 + 30 × Q + Q2
Задача №118. Расчёт цены монополиста
Монополия на рынке имеет следующую функцию предельных издержек:
МС = - 10 + 3 × Q.
Предельный доход выражен функцией:
MR = 40 - 2 × Q.
Какова цена, назначаемая монополией за свой продукт на рынке?
Задача №119. Расчёт фиксированных затрат монополиста
Даны функция спроса на продукцию монополиста
Q = 25 - P
и функция средних переменных затрат
AVC = 4 + 0,5 × Q.
Известно, что максимум прибыли монополиста равен 23,5. Найти его фиксированные затраты.

Экономическая прибыль

Счёт операций с капиталом

Счёт использования располагаемого дохода
Задача №122. Расчёт эластичности спроса по цене
Функция спроса на продукцию монополиста:
P = 20 - 2 × Q,
MC = AC = 4.
Найти эластичность спроса по цене, если монополист ищет максимум прибыли.
Задача №126. Расчёт монопольной цены
Монополист, производящий табуретки, максимизирует прибыль. Какую он назначит цену, если общие издержки составляют TC = 20 × Q + 100, а эластичность спроса по цене постоянна и равна -2?
Задача №127. Расчёт прибыли, оптимальной цены и выпуска продукции
Допустим, общие затраты монополии равны
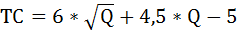
при спросе на её продукцию
Q = 32 – 4 × Р.
Найти оптимальную цену и выпуск продукции, обеспечивающие наибольшую прибыль. Вычислить эту прибыль.
Задача №129. Расчёт предельных издержек
Определите предельные издержки, если переменные издержки изменились с 1400 до 1650 рублей, а объем продукции вырос с 420 до 470 единиц.
Задача №130. Расчёт издержек
Заполните пустые ячейки по имеющимся данным:
| Q | TC | FC | VC | AFC | AVC | ATC | MC |
| 0 | |||||||
| 1 | 148 | ||||||
| 2 | 64 | 28 | |||||
| 3 | 66 | ||||||
| 4 | 224 |




















