Задача №58. Расчёт индексов структурных сдвигов
В таблице представлены данные о среднесписочной численности и среднемесячном фонде оплаты труда по категориям персонала.
Определите:
1) изменение средней заработной платы в целом по организации (индекс переменного состава);
2) влияние изменения уровня оплаты труда на среднюю заработную плату (индекс фиксированного состава);
3) влияние изменений в структуре персонала на среднюю заработную плату (индекс структурных сдвигов).
| Категории персонала | 2014 год | 2015 год | ||
|---|---|---|---|---|
| Среднесписочная численность, чел., Т0 | Среднемесячная заработная плата одного работника, тыс. руб., Х0 | Среднесписочная численность, чел., Т0 | Среднемесячная заработная плата одного работника, тыс. руб., Х1 | |
| Основной | 125 | 31,2 | 130 | 34,6 |
| Вспомогательный | 18 | 25,8 | 16 | 27,4 |
| В целом | 143 | - | 146 | - |
Решение:
1. Изменение средней заработной платы в целом по организации (индекс переменного состава) рассчитаем по формуле:
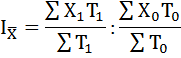
где
T1, T0 - среднесписочная численность отдельных категорий персонала (или всего персонала предприятия, отрасли) в отчётном и базисном периоде;
X1, X0 – средняя зарплата по категориям персонала (по предприятиям и отраслям) в отчётном и базисном периоде.
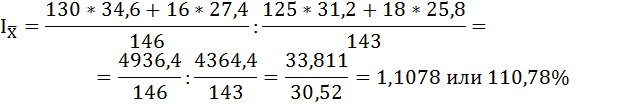
средняя заработная плата одного работника по обеим категориям персонала возросла на 10,78%.
2. Влияние изменения уровня оплаты труда на среднюю заработную плату (индекс фиксированного состава) определим по формуле:
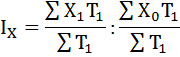
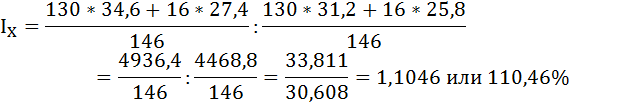
Это означает, что в среднем по двум категориям персонала заработная плата повысилась на 10,46%.
3. Влияние изменений в структуре персонала на среднюю заработную плату (индекс структурных сдвигов) определим по формуле:
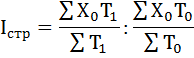
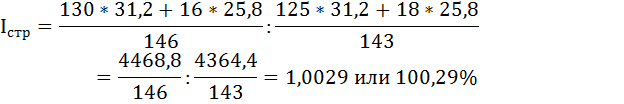
Средняя зарплата одного работника по обеим категориям персонала возросла на 0,29% за счёт изменения удельного веса отдельных категорий в общем числе сотрудников предприятия.
Проверим расчёты, используя взаимосвязь трёх индексов:
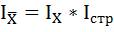
1,1078 = 1,1046 × 1,0029
1,1078 = 1,1078 - тождество верное.
Смотри ещё























