Задача №83. Расчёт прибыли
Найти выпуск, обеспечивающий минимум средних затрат при МС = 2 × Q – 10, FC = 100. Сравнить прибыль при этом выпуске с максимальной прибылью при Р = 20.
Решение:
1. Найдём функцию общих затрат TC, зная её производную. Для этого рассчитаем первообразную от функции предельных затрат МС:
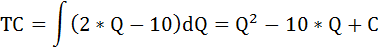
где
С – константа, равная величине постоянных затрат.
Таким образом функция общих затрат имеет вид:
ТС = Q2 – 10Q + 100.
Найдём функцию средних затрат по формуле:
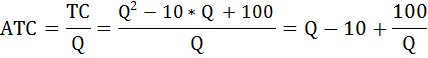
Для нахождения экстремума (минимума средних затрат) функции приравняем к нулю её производную.
Производная функции средних затрат равна:
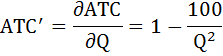
Приравняем её к нулю:
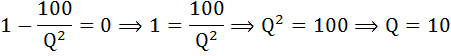
Итак, выпуск Q = 10 обеспечивает минимум средних затрат:
АТС = 10-10+10=10
2. Расчёт прибыли произведём по формуле, учитывая, что P = 20:
П = TR – TC = PQ – (Q2 – 10Q + 100) = 20 × Q – (Q2 – 10Q + 100) =
= 20 × Q – Q2 + 10 × Q – 100 = – Q2 + 30Q – 100,
где
TR - общий доход или выручка, равная произведению цены на количество выпущенной продукции.
При Q = 10 прибыль будет равна:
П = – 100 + 30 × 10 – 100 = 100.
Определим объём выпуска, при котором прибыль будет максимальной. Другими словами найдём экстремум функции прибыли. Для этого найдём производную функции прибыли и приравняем её к нулю.
П’ = (– Q2 + 30Q – 100)’ = – 2Q + 30
– 2Q + 30 = 0
Q = 15
Итак, выпуск Q = 15 обеспечивает максимум прибыли. Найдём величину прибыли, подставив это значение в функцию прибыли.
П = – Q2 + 30Q – 100 = – 225 + 30 × 15 – 100 = 125
Делаем вывод: при Q = 10, когда средние затраты минимальны, П = 100;
при Q = 15, когда прибыль максимальна, она равна 125. Следовательно, недополученная прибыль будет равна 25.
Смотри ещё
- Анализ рыночной структуры / Задача № 152. Расчёт оптимального объёма выпуска, цены и прибыли монополиста
- Анализ рыночной структуры / Задача №153. Расчёт индекса Лернера
- Анализ рыночной структуры / Задача №154. Расчёт равновесной цены, объёма выпуска и прибыли
- Анализ рыночной структуры / Задача №155. Расчёт объема продаж, цены и прибыли фирмы монополистического конкурента
- Анализ рыночной структуры / Задача №156. Расчёт рыночной цены и оптимальный объём выпуска
- Анализ рыночной структуры / Задача №157. Расчёт оптимального выпуска и цены фирмы монополиста
- Анализ рыночной структуры / Задача №158. Расчёт избыточной мощности фирмы
- Анализ рыночной структуры / Задача №159. Расчёт оптимального выпуска и цены до и после рекламной кампании
- Анализ рыночной структуры / Задача №168. Расчёт объема выпуска продукции
- Анализ рыночной структуры / Задача №174. Расчёт параметров равновесия на рынке монополистической конкуренции
- Анализ рыночной структуры / Задача №183. Расчёт индекса Лернера
- Анализ рыночной структуры / Задача №188. Расчёт параметров рыночного равновесия по Курно
- Анализ рыночной структуры / Задача №189. Расчёт избыточной производственной мощности
- Анализ рыночной структуры / Задача №197. Расчёт выпуска и цены лидера
- Анализ рыночной структуры / Задача №198. Лидерство в ценообразовании
- Анализ рыночной структуры / Задача №199. Расчёт ущерба от монополии
- Анализ хозяйственной деятельности / Задача №5. Расчёт изменения общей себестоимости продукции за счет влияния факторов и их долевое участие в общем изменении
- Макроэкономическая нестабильность / Задача №33. Расчёт реального дохода вкладчика с учётом инфляции
- Макроэкономическая нестабильность / Задача №83. Расчёт реального дохода
- Мировая экономика / Задача №1. Определение сравнительных преимуществ
- Основные макроэкономические показатели / Задача №16. Расчёт ВВП (двумя способами), ВНП, ЧНП, НД, ЛД, РЛД и др
- Основные макроэкономические показатели / Задача №19. Расчёт ВВП, ВНП, ЧВП, ЧНП, НД, ЛД, РЛД и др.
- Основные макроэкономические показатели / Задача №22. Расчёт национального дохода
- Основные макроэкономические показатели / Задача №23. Расчёт национального дохода
- Основные макроэкономические показатели / Задача №24. Расчёт личного дохода
- Основные макроэкономические показатели / Задача №26. Расчёт ВВП по доходам
- Основные макроэкономические показатели / Задача №78. Расчёт изменения расходов на личное потребление
- Поведение потребителя / Задача №58. Расчёт дохода потребителя
- Провалы рынка и государственное регулирование / Задача №194. Расчёт общественно оптимального уровня производства фирмы
- Производство и затраты фирмы / Задача №71. Расчёт затрат























