Задача №77. Расчёт коэффициента Джини
Предположим, что в некоторой стране N проживают три группы населения: бедные, средний класс и богатые. Группы равны по численности жителей, но различаются по уровню дохода: средний класс зарабатывает в два раза больше, чем бедные, а богатые зарабатывают в два раза больше, чем средний класс. Внутри групп доходы распределены равномерно. Совокупный доход всех жителей страны равен Y. Нарисуйте график кривой Лоренца и рассчитайте индекс Джини.
Решение:
Третья часть населения, по условию задачи, бедные. Их доходы обозначим через х.
Тогда 2х – величина доходов среднего класса,
4х - величина доходов богатых.
Следовательно, совокупный доход всех жителей страны Y состоит из 7 одинаковых частей.
1/7 – доля доходов бедных,
2/7 – доля доходов среднего класса,
4/7 – доля доходов богатых.
Представим условие задачи в табличной форме:
| Социальная группа населения | Доля населения, xi | Доля в общем объёме денежных доходов, уi | Расчётные величины
|
||
|---|---|---|---|---|---|
| Кумулятивная доля дохода, cum yi | xi cum yi | xi уi | |||
| Бедные | 0,333 | 0,1429 | 0,1429 | 0,0475724 | 0,0475724 |
| Средний класс |
0,333 | 0,2857 | 0,4286 | 0,1427138 | 0,0951414 |
| Богатые | 0,333 | 0,5714 | 1,0000 | 0,333 | 0,1902862 |
| Итого | 1,000 | 1,0000 | - | 0,5232862 | 0,333 |
Построим кривую Лоренца:
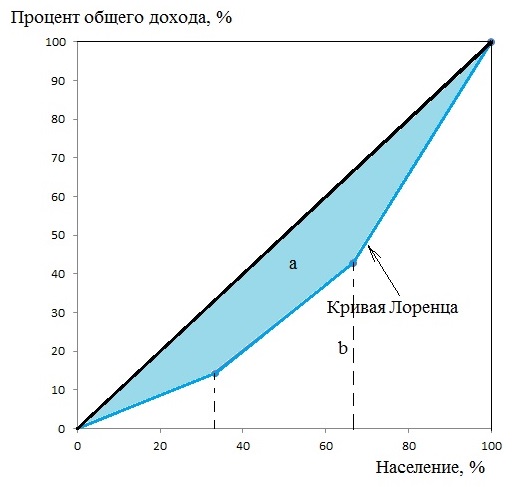
Индекс Джини рассчитаем двумя способами.
1) Способ аналитический. Коэффициент Джини рассчитывается по формуле:
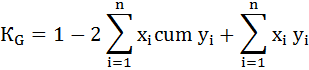
где
xi – доля населения, принадлежащая к i-й социальной группе в общей численности населения;
уi – доля доходов, сосредоточенная у i-й социальной группы населения;
n – число социальных групп;
cum yi – кумулятивная доля дохода.
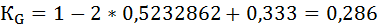
2) Способ геометрический. Коэффициент Джини определяется как отношение площади фигуры, образуемой кривой Лоренца и линией равномерного распределения (Sa), к площади треугольника ниже линии равномерного распределения (Sa+b):
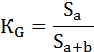
Площадь фигуры, образуемой кривой Лоренца и линией равномерного распределения (Sa) легко найти вычитанием из площади треугольника (Sa+b) площадь фигуры, лежащей ниже кривой Лоренца.
Площадь фигуры b, лежащей ниже кривой Лоренца можно разбить на треугольник и две трапеции:
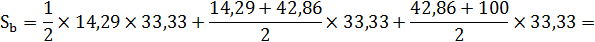
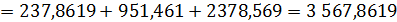
Площадь фигуры a будет равна:
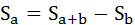
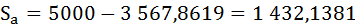
Индекс Джини будет равен:
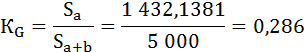
Оба способа дали одинаковый результат.
Как видно из таблицы, наиболее обеспеченная группа населения сконцентрировала 57,14% доходов, а доля наименее обеспеченной группы в общем доходе составила 14,29%.

Экономическая прибыль

Счёт операций с капиталом
Смотри ещё
- Основные макроэкономические показатели / Задача №26. Расчёт ВВП по доходам
- Основные макроэкономические показатели / Задача №63. Расчёт частных сбережений
- Распределение дохода / Задачи №76. Расчёт коэффициента Джини
- Статистика уровня жизни населения / Задача № 34. Расчёт коэффициента Джини
- Фискальная политика / Задача №41. Определение состояния государственного бюджета
- Фискальная политика / Задача №42. Определение состояния государственного бюджета

Счёт использования располагаемого дохода




















