Задача №57. Расчёт индексов структурных сдвигов
Имеются следующие данные по двум отраслям:
| Отрасли | Среднемесячная заработная плата одного работника, руб. | Среднесписочная численность работников, чел. | ||
|---|---|---|---|---|
| Базисный период | Отчётный период | Базисный период | Отчётный период | |
| 1 | 4900 | 5200 | 100 | 120 |
| 2 | 6160 | 7200 | 200 | 370 |
Определите:
1. индексы средней месячной заработной платы по каждой отрасли;
2. индекс заработной платы переменного состава, индекс постоянного состава, индекс структурных сдвигов;
3. изменение фонда оплаты труда в целом по двум отраслям и по каждой отрасли в отдельности за счёт изменения средней заработной платы и среднесписочной численности работников.
Сделайте выводы.
Решение:
1) Индекс средней месячной заработной платы по 1 отрасли:
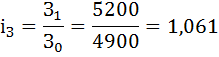
Индекс средней месячной заработной платы по 2 отрасли:
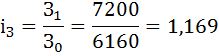
2) Средняя месячная заработная плата по двум заводам в базисном периоде составила:
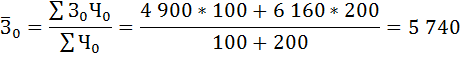
Средняя месячная заработная плата по двум заводам в отчётном периоде составила:
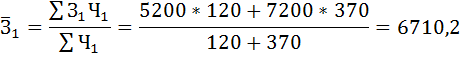
Индекс переменного состава:
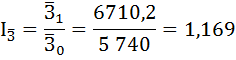
средняя заработная плата по двум отраслям возросла на 16,9%.
Индекс структурных сдвигов характеризует влияние изменения структуры изучаемого явления на динамику среднего уровня индексируемого показателя и рассчитывается по формуле:
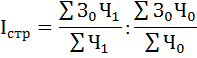
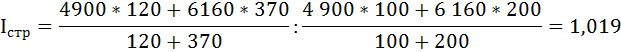
Средняя заработная плата по двум отраслям возросла на 1,9% за счёт изменения удельного веса численности работников.
Индекс постоянного состава представляет собой отношение средних взвешенных с одними и теми же весами (при постоянной структуре). Индекс постоянного состава учитывает изменение только индексируемой величины и показывает средний размер изменения изучаемого показателя у единиц совокупности.
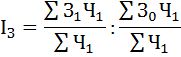
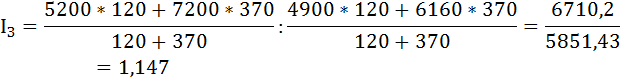
Можно воспользоваться системой взаимосвязанных индексов:
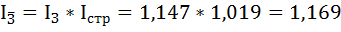
3) Величина фонда оплаты труда определяется как произведение численности работников и средней заработной платы.
F = З × Ч
Рассчитаем ФОТ по каждой отрасли в отдельности и в целом по двум отраслям. Результаты вычислений занесём в таблицу.
| Отрасли | Фонд оплаты труда, тыс. руб. | Абсолютное изменение фонда оплаты труда, тыс. руб. | |
|---|---|---|---|
| Базисный период | Отчётный период | ||
| 1 | 490 | 624 | 134 |
| 2 | 1232 | 2664 | 1432 |
| Итого | 1722 | 3288 | 1566 |
Изменение фонда оплаты труда в отчётном периоде по сравнению с базисным периодом зависит от двух факторов:
а) изменения численности работников (Ч)
ΔF(Ч) = ΔЧ × З0 = (490 – 300) × 5740 = 1 090,6 тыс. руб.,
б) изменения среднего уровня заработной платы (З).
ΔF(З) = ΔЗ × Ч1 = (6710,2 – 5740) × 490 = 475,4 тыс. руб.
В целом изменение фонда оплаты труда в отчётном периоде по сравнению с базисным периодом составило:
ΔF = ΔF(Ч) + ΔF(З) = 1 090,6 + 475,4 = 1 566 тыс. руб.
Выводы: если бы произошедшие изменения средней заработной платы не сопровождались структурными перераспределениями численности рабочих, то средняя заработная плата по двум отраслям возросла бы на 10,3%.
Изменение структуры численности работников двух отраслей в общей численности работников вызвало рост средней заработной платы на 1,9%. Одновременное воздействие двух факторов увеличило среднюю заработную плату по двум отраслям на 16,9%.
Фонд оплаты труда в отчётном периоде по сравнению с базисным увеличился на 1566 тыс. руб., в том числе за счёт изменения численности работников на 1 090,6 тыс. руб. и за счёт изменения среднего уровня заработной платы на 475,4 тыс. руб.
Смотри ещё























