Задача №52. Расчёт минимальной численности генеральной совокупности

На основе случайной бесповторной выборки планируется 10%-ное обследование доли различных признаков, характеризующих население области. Какова должна быть минимальная численность населения области, чтобы предельная ошибка выборки с вероятностью 0,997 при определении доли всех подлежащих регистрации признаков не превышала 0,5%?

Решение:

Необходимо определить минимальную численность населения области для обследования доли различных признаков, характеризующих население области, то есть не что иное, как численность генеральной совокупности (N).

10%-ное обследование означает, что из численности населения области будет отобрана 1/10 часть.

n = 0,1 × N

При вероятности 0,997 коэффициент доверия равен t = 3.

Предельная ошибка выборки по условию:

Δ_ω = 0,005

При случайном бесповторном отборе для рассчёта необходимой численности выборки для определения доли с заданной точностью, применяется следующая формула:

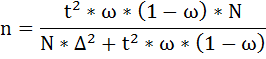
Так как в условии задачи величина дисперсии не задана, берём ω = 0,5.

Подставив имеющиеся в условии данные, получаем уравнение с двумя неизвестными:

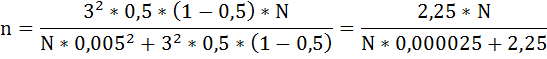
Так как левая часть уравнения равна 0,1 × N, произведём замену и выразим N:

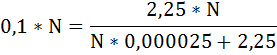
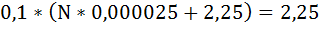
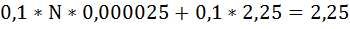
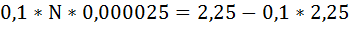
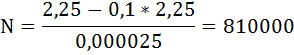
Ответ: минимальная численность населения области должна быть как минимум равна 810 000 человек.