Задача №39. Расчёт предела, в котором находятся средние затраты времени
Для выявления затрат времени на обработку деталей рабочими разных квалификаций на заводе была произведена 10%-ная типическая выборка пропорционально численности выделенных групп (внутри типичных по специальности групп произведен случайный бесповторный отбор данных о затратах времени на обработку одной детали). Результаты обследования представлены в таблице:
| Группы рабочих по квалификации | Число рабочих в выборке | Средние затраты времени на обработку одной детали (минут) | Среднее квадратическое отклонение |
|---|---|---|---|
| I | 60 | 10 | 1 |
| II | 120 | 14 | 4 |
| III | 80 | 20 | 2 |
| IV | 40 | 25 | 6 |
С вероятностью 0,954 определите предел, в котором находятся средние затраты времени на обработку деталей рабочими завода.
Решение:
Объем выборки в каждой типической группе:
n1 = 60 рабочих,
n2 = 120 рабочих,
n3 = 80 рабочих,
n4 = 40 рабочих.
Рассчитаем общую выборочную среднюю из групповых выборочных средних путем взвешивания последних по численности отобранных групп:
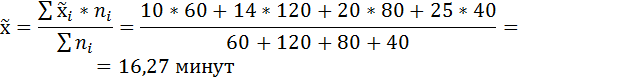
Средние затраты времени на обработку одной детали в выборке составляют 16,27 минут.
Определим среднюю дисперсию из внутригрупповых дисперсий:
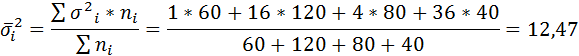
Рассчитаем среднюю ошибку выборочной средней при 10%-ной типической выборке:
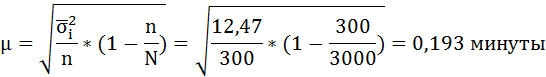
Определим предельную ошибку выборочной средней с вероятностью 0,954.
При Р = 0,954, t = 2 (значения t для других Р смотрите здесь).
Δ = t × µ = 2 × 0,193 = 0,387 минуты
16,27 – 0,387 ˂ 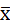 ˂ 16,27 + 0,387
˂ 16,27 + 0,387
С вероятностью 0,954 можно утверждать, что на заводе средние затраты времени на обработку одной детали колеблются от 15,88 до 16,65 минут.
Смотри ещё
- Выборочное наблюдение / Задача №32. Расчёт предела, в котором находится средний возраст рабочих
- Выборочное наблюдение / Задача №33. Расчёт предела, в котором находится средняя крепость пряжи в партии
- Выборочное наблюдение / Задача №36. Расчёт необходимой численности выборки при механическом отборе
- Выборочное наблюдение / Задача №37. Расчёт необходимой численности выборки
- Выборочное наблюдение / Задача №38. Расчет необходимой численности выборки для определения доли
- Выборочное наблюдение / Задача №51. Расчёт ошибки выборочной доли
- Средние величины и показатели вариации / Задача №6. Расчёт показателей вариации
- Средние величины и показатели вариации / Задача №7. Расчёт коэффициента вариации
- Средние величины и показатели вариации / Задача №8. Расчёт средней
- Средние величины и показатели вариации / Задача №9. Расчёт среднего квадрата индивидуальных значений признака
- Средние величины и показатели вариации / Задача №10. Расчёт среднего квадрата отклонений вариантов признака от произвольной величины
- Средние величины и показатели вариации / Задача №11. Расчёт дисперсии признака
- Средние величины и показатели вариации / Задача №12. Расчёт коэффициента вариации
- Средние величины и показатели вариации / Задача №13. Расчёт среднего квадрата отклонений индивидуальных значений признака от произвольной величины
- Средние величины и показатели вариации / Задача №22. Виды дисперсии и их расчёт
- Средние величины и показатели вариации / Задача №23. Расчёт показателей асимметрии и эксцесса
- Средние величины и показатели вариации / Задача №24. Расчёт показателей вариации по несгруппированным данным
- Средние величины и показатели вариации / Задача №29. Расчёт крайних значений вариационного ряда
- Средние величины и показатели вариации / Задача №30. Расчёт коэффициента вариации
- Средние величины и показатели вариации / Задача №43. Расчёт описательных статистик
- Средние величины и показатели вариации / Задача №45. Расчёт абсолютных и относительных показателей вариации
- Средние величины и показатели вариации / Задача №48. Расчёт показателей вариации
- Статистические методы изучения взаимосвязей / Задача №47. Построение модели линейной регрессии
- Эконометрика / Задача №1 Построение уравнения регрессии
- Эконометрика / Задача №4. Построение регрессионной модели с использованием фиктивной переменной
- Эконометрика / Задача №5. Построение автокорреляционной функции























