Задача №34. Расчёт пределов доли признака в генеральной совокупности
Для изучения мнения студентов о проведении определенных мероприятий из совокупности, состоящей из 10 тыс. человек, методом случайного бесповторного отбора опрошено 600 студентов. Из них 240 одобрили план мероприятий. С вероятностью 0,954 определите предел, в котором находится доля студентов, одобривших мероприятия, во всей совокупности.
Решение:
При собственно-случайном бесповторном отборе среднюю ошибку выборочной доли рассчитывают по формуле:
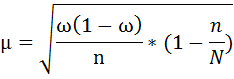
где
ω - доля единиц выборочной совокупности, обладающих изучаемым признаком,
n – численность выборочной совокупности,
N – численность генеральной совокупности.
Доля студентов одобривших мероприятия из числа опрошенных студентов составила:
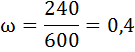
Рассчитаем среднюю ошибку выборочной доли:
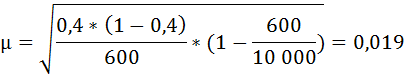
Предельная ошибка выборочной доли с вероятностью 0,954 составит:
Δ = μ * t = 0,019 * 2 = 0,039 (или 3,9%).
t - коэффициент доверия.
Значение t табличное (смотри Задачу №32).
При Р = 0,954, t = 2,0.
Определим пределы, доли признака в генеральной совокупности следующим образом:
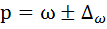
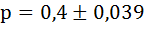
Пределы генеральной доли признака в генеральной совокупности:
0,4 – 0,039 ˂ р ˂ 0,4 + 0,039
или
0,361 ˂ р ˂ 0,439
С вероятностью 0,954 можно утверждать, что доля студентов, одобривших мероприятия, во всей совокупности находится в пределах от 36,1% до 43,9%.

Совершенная конкуренция
Смотри ещё
- Выборочное наблюдение / Задача №32. Расчёт предела, в котором находится средний возраст рабочих
- Выборочное наблюдение / Задача №33. Расчёт предела, в котором находится средняя крепость пряжи в партии
- Выборочное наблюдение / Задача №35. Расчёт предела доли признака в генеральной совокупности
- Выборочное наблюдение / Задача №36. Расчёт необходимой численности выборки при механическом отборе
- Выборочное наблюдение / Задача №37. Расчёт необходимой численности выборки
- Выборочное наблюдение / Задача №38. Расчет необходимой численности выборки для определения доли
- Выборочное наблюдение / Задача №39. Расчёт предела, в котором находятся средние затраты времени
- Выборочное наблюдение / Задача №51. Расчёт ошибки выборочной доли
- Выборочное наблюдение / Задача №52. Расчёт минимальной численности генеральной совокупности

Экономическая прибыль

Счёт операций с капиталом




















